Đề kiểm tra Cuối kì 1 Toán 8 CD có đáp án (Đề 2)
-
279 lượt thi
-
20 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 7:
Cho hai đường thẳng và Với điều kiện nào sau đây thì hai đường thẳng d và d’ cắt nhau?
 Xem đáp án
Xem đáp án
Chọn đáp án C
Câu 8:
Cho đường thẳng y = ax + b Với giá trị a thỏa mãn điều kiện nào sau đây thì góc tạo bởi đường thẳng đó với trục Ox là góc nhọn?
 Xem đáp án
Xem đáp án
Chọn đáp án C
Câu 9:
Tổng số cạnh bên và cạnh đáy của một hình chóp tam giác đều là
 Xem đáp án
Xem đáp án
Chọn đáp án B
Câu 10:
Một hình chóp tứ giác đều có độ dài trung đoạn là a, diện tích xung quanh là thì có độ dài cạnh đáy là
 Xem đáp án
Xem đáp án
Chọn đáp án C
Câu 11:
Tứ giác ABCD có số đo các góc tỉ lệ thuận với 4;3;5;6. Khi đó số đo là
 Xem đáp án
Xem đáp án
Chọn đáp án B
Câu 14:
a) Viết điều kiện xác định của biểu thức A
 Xem đáp án
Xem đáp án
a) Ta có
với mọi x
Điều kiện xác định của biểu thức A là hay và , tức là và
Vậy điều kiện xác định của biểu thức A là và
Câu 16:
c) Tính giá trị của biểu thức A biết |x + 3| = 1
 Xem đáp án
Xem đáp án
c) Ta có suy ra hoặc
Do đó (không thỏa mãn điều kiện) hoặc (thỏa mãn điều kiện)
Thay vào biểu thức ta được:
Vậy khi
Câu 17:
Một thiết bị tiệt khuẩn y tế bằng năng lượng mặt trời được mua với giá 60 triệu đồng, mỗi năm thiết bị tiệt khuẩn đó đều khấu hao k (triệu đồng) với 0 < k < 60. Gọi y (triệu đồng) là giá của thiết bị tiệt khuẩn đó sau x năm sử dụng.
a) Chứng tỏ rằng y là hàm số bậc nhất của x, tức là
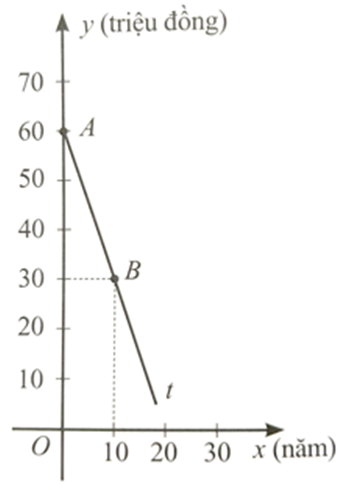
b) Trong hình vẽ bên, tia At là một phần của đường thẳng y = ax + b. Tìm a, b. Từ đó, cho biết sau 12 năm sử dụng thì giá của thiết bị tiệt khuẩn đó bằng bao nhiêu phần trăm so với giá mua ban đầu.
 Xem đáp án
Xem đáp án
a) Sau x năm sử dụng, thiết bị tiệt khuẩn đó bị khấu hhao là kx (triệu đồng).
Giá của thiết bị tiệt khuẩn đó sau x năm sử dụng là: y = 60 - kx hay y = -kx + 60.
Mà 0 < k < 60 hay suy ra y là hàm số bậc nhất của x.
b) Từ câu a, ta có
Do đường thẳng đi qua điểm B( 10;30) nên ta có:
Hay
Suy ra
Khi đó, đường thẳng cần tìm là:
Giá của thiết bị tiệt khuẩn đó sau 12 năm sử dụng là:
(triệu đồng).
Tỉ số phần trăm giữa giá của thiết bị tiệt khuẩn đó sau 12 năm sử dụng và giá mua ban đầu là:
Vậy sau 12 năm sử dụng thì giá của thiết bị tiệt khuẩn đó bằng 40% so với giá mua ban đầu.
Câu 18:
Cho hình chóp tam giác đều S.ABC có cạnh đáy AB = 5 cm và độ dài trung đoạn SI = 6 cm (hình vẽ bên). Tính:
a) Diện tích xung quanh và diện tích toàn phần của hình chóp S.ABC
b) Thể tích của hình chóp S.ABC, biết chiều cao SO của hình chóp là 5,8 cm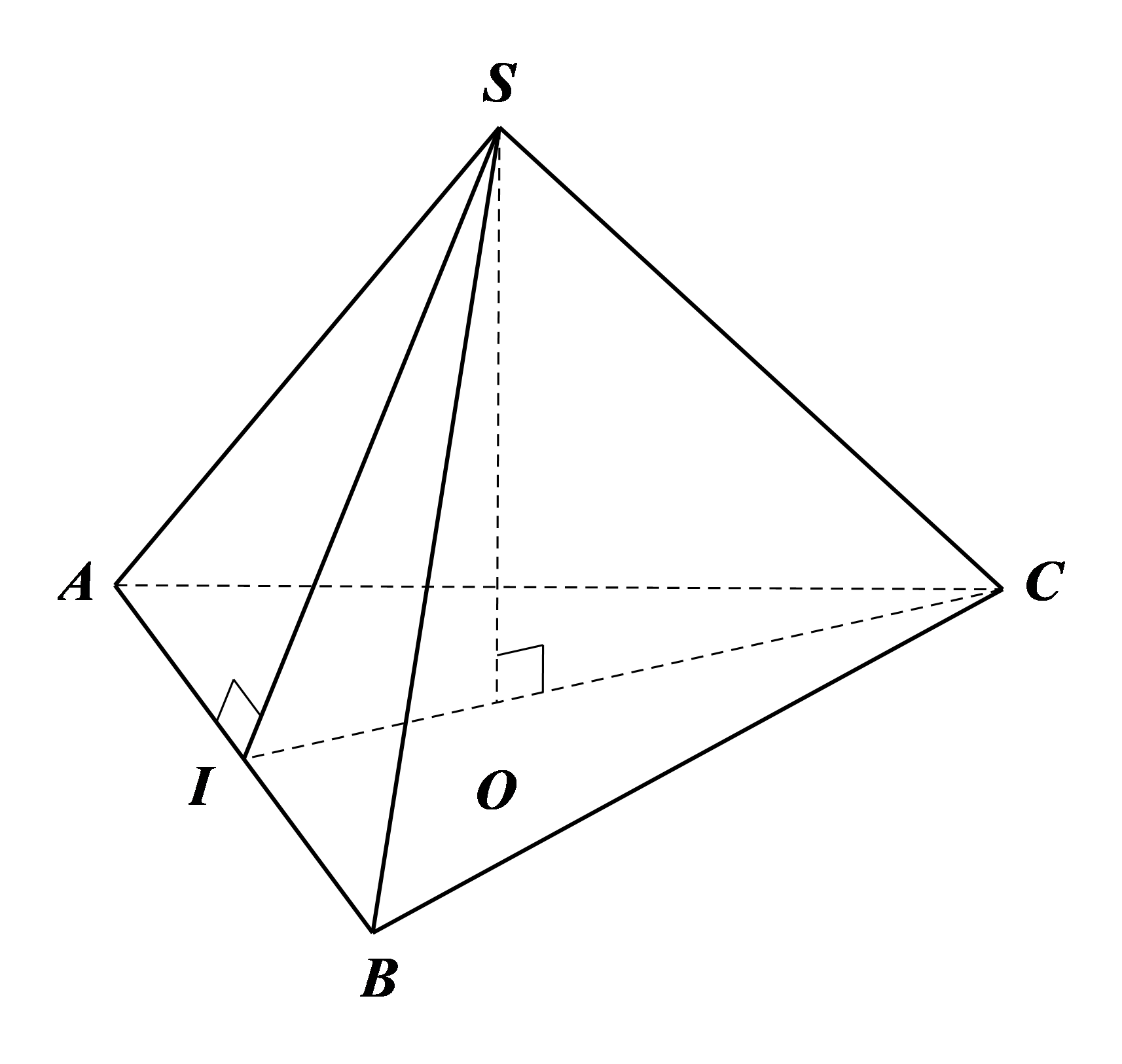
 Xem đáp án
Xem đáp án
a) Diện tích xung quanh của hình chóp tam giác đều S.ABC là:
Tam giác ABC là tam giác đều nên đường trung tuyến CI đồng thời là đường cao.
Xét vuông tại I có
Suy ra
Do đó
Diện tích đáy của hình chóp tam giác đều S.ABC là:
Diện tích toàn phần của hình chóp tam giác đều S.ABC là:
b) Thể tích của hình chóp tam giác đều S.ABC là:
Câu 19:
Cho hình bình hành ABCD có BC = 2AB, Gọi E, F theo thứ tự là trung điểm của BC, AD. Trên tia AB lấy điểm I sao cho B là trung điểm của AI.
a) Tứ giác ABEF là hình gì? Vì sao?
b) Tính
 Xem đáp án
Xem đáp án
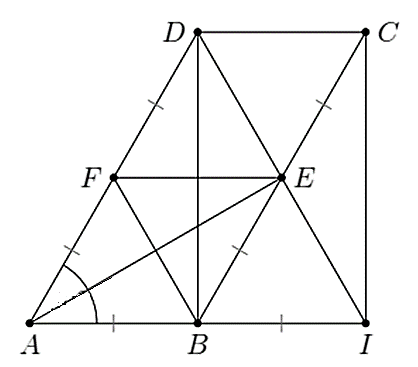
a) Do tứ giác ABCD là hình bình hành nên .
Vì và (do F là trung điểm của nên
Tứ giác ABEF có BE = AF và (vì
Suy ra, tứ giác ABEF là hình bình hành.
Do E là trung điểm của BC nên hay
Vì và nên .
Hình bình hành ABEF có AB = BE nên ABEF là hình thoi.
b) Vì tứ giác ABCD là hình bình hành nên .
Vì và (do B là trung điểm của AI) nên BI = CD .
Tứ giác BICD có BI // CD (vì AB // CD ) và BI = CD nên tứ giác BICD là hình bình hành.
Ta thấy BD vừa là đường trung tuyến vừa là đường phân giác của tam giác ADI nên tam giác ADI cân tại D .
Suy ra BD cũng là đường cao của tam giác ADI nên hay
Hình bình hành BICD có nên tứ giác BICD là hình chữ nhật.
Khi đó, E là trung điểm của hai đường chéo BC và DI .
Tam giác ADI cân tại D có nên tam giác ADI là tam giác đều.
là tam giác đều có AE là đường trung tuyến nên đồng thời là đường cao.
Do đó, hay .
Câu 20:
Cho Chứng minh rằng:
 Xem đáp án
Xem đáp án
Theo giả thiết,
Suy ra
Suy ra hoặc hoặc
⦁ Nếu thì khi đó
Ta có
Do đó
⦁ Nếu hoặc chứng minh tương tự ta cũng có
Vậy nếu thì