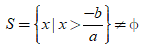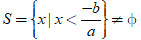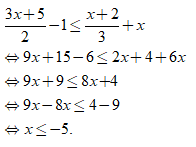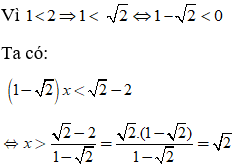Bài tập Bài 4: Bất phương trình bậc nhất một ẩn
-
3393 lượt thi
-
10 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Bất phương trình ax + b > 0 vô nghiệm khi
Xem đáp án
Nếu a > 0 thì ax + b > 0 ⇔ x > - b/a nên
Nếu a < 0 thì ax + b > 0 ⇔ x < - b/a nên
Nếu a = 0 thì ax + b > 0 có dạng 0x + b > 0
Với b > 0 thì S = R.
Với b ≤ 0 thì S = Ø
Chọn đáp án D.
Câu 2:
Tập nghiệm S của bất phương trình: là?
Xem đáp án
Ta có: 5x - 1 ≥ (2x)/5 + 3 ⇔ 25x - 5 ≥ 2x + 15 ⇔ 23x ≥ 20 ⇔ x ≥ 20/23.
Vậy tập nghiệm của bất phương trình là x ≥ 20/23;
Chọn đáp án D.
Câu 3:
Bất phương trình có bao nhiêu nghiệm nguyên lớn hơn -10
Xem đáp án
Ta có:
Vì x ∈ Z, - 10 < x ≤ - 5 nên có 5 nghiệm nguyên.
Chọn đáp án B.
Câu 4:
Tập nghiệm S của bất phương trình: là?
Xem đáp án
Vậy tập nghiệm của bất phương trình là:
Chọn đáp án B.
Câu 7:
Giải bất phương trình: 8x + 4 > 2(x+ 5).
Xem đáp án
Ta có:
8x + 4 > 2( x +5 )
⇔ 8x + 4 > 2x + 10
⇔ 8x – 2x > 10 - 4
⇔ 6x > 6
⇔ x > 6 : 6
⇔ x > 1
Chọn đáp án D
Câu 10:
Tìm m để x = 2 là nghiệm bất phương trình: mx + 2 < x + 3 + m
Xem đáp án
Do x = 2 là nghiệm của bất phương trình đã cho nên:
2m + 2 < 2 + 3 + m
⇔ 2m – m < 2 + 3- 2
⇔ m < 3
Chọn đáp án B