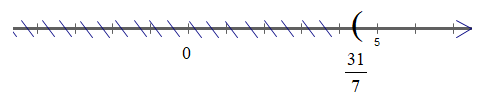
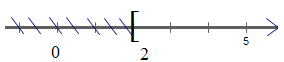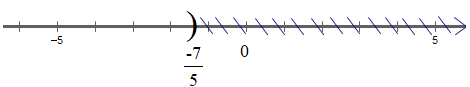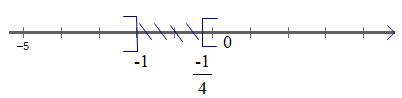28 câu hỏi trắc nghiệm thuộc Dạng 2: Phiếu 1 có đáp án

Câu 1:

Giải các phương trình sau

3 - 4 x + 24 + 6 x = x + 27 + 3 x

Xem đáp án

$3 - 4 x + 24 + 6 x = x + 27 + 3 x$

$\begin{array}{l} \Leftrightarrow - 4 x + 6 x - x - 3 x = 27 - 24 - 3 \\ \Leftrightarrow - 2 x = 0 \Rightarrow x = 0 \end{array}$

$S = \{0\}$

Câu 2:

2.

\frac{2 x + 3}{4} - \frac{5 x + 3}{6} = \frac{3 - 4 x}{12}

Xem đáp án

$\frac{2 x + 3}{4} - \frac{5 x + 3}{6} = \frac{3 - 4 x}{12}$

$\begin{array}{l} \Leftrightarrow \frac{3. (2 x + 3)}{12} - \frac{2. (5 x + 3)}{12} = \frac{3 - 4 x}{12} \\ \Leftrightarrow \frac{6 x + 9 - 10 x - 6}{12} = \frac{3 - 4 x}{12} \\ \Leftrightarrow \frac{3 - 4 x}{12} = \frac{3 - 4 x}{12} \\ \Leftrightarrow 3 - 4 x = 3 - 4 x \\ \Leftrightarrow - 4 x + 4 x = 3 - 3 \\ \Leftrightarrow 0. x = 0 \\ \Rightarrow x \in ℝ \\ S = \{x | x \in ℝ\} \end{array}$

Câu 3:

3.

(2 x + 5) (x - 4) + 3 (x - 4) = 0

Xem đáp án

$(2 x + 5) (x - 4) + 3 (x - 4) = 0$

$\begin{array}{l} \Leftrightarrow (x - 4) (2 x + 5 + 3) = 0 \\ \Leftrightarrow (x - 4) (2 x + 8) = 0 \\ \Leftrightarrow [\begin{array}{l} x - 4 = 0 \\ 2 x + 8 = 0 \end{array} \Leftrightarrow [\begin{array}{l} x = 4 \\ x = - 4 \end{array} \\ S = \{- 4; 4\} \end{array}$

Câu 4:

4.

2 {(3 x + 5)}^{2} = (3 x + 5) (x - 7)

Xem đáp án

$2 {(3 x + 5)}^{2} = (3 x + 5) (x - 7)$

$\begin{array}{l} \Leftrightarrow (3 x + 5) (6 x + 10 - x + 7) = 0 \\ \Leftrightarrow (3 x + 5) (5 x + 17) = 0 \\ \Leftrightarrow [\begin{array}{l} 3 x + 5 = 0 \\ 5 x + 17 = 0 \end{array} \Leftrightarrow [\begin{array}{l} x = \frac{- 5}{3} \\ x = \frac{- 17}{5} \end{array} \\ S = \{\frac{- 5}{3}; \frac{- 17}{5}\} \end{array}$

Câu 5:

$5 . 9 {(2 x - 1)}^{2} - 4 {(x + 1)}^{2} = 0$

Xem đáp án

$9 {(2 x - 1)}^{2} - 4 {(x + 1)}^{2} = 0$

$\begin{array}{l} \Leftrightarrow 9 (4 x^{2} - 4 x + 1) - 4 (x^{2} + 2 x + 1) = 0 \\ \Leftrightarrow {[3 (2 x - 1)]}^{2} - {[2 (x + 1)]}^{2} = 0 \\ \Leftrightarrow (6 x - 3 + 2 x + 2) (6 x - 3 - 2 x - 2) = 0 \\ \Leftrightarrow (4 x - 5) (8 x - 1) = 0 \\ \Leftrightarrow [\begin{array}{l} 4 x - 5 = 0 \\ 8 x - 1 = 0 \end{array} \Leftrightarrow [\begin{array}{l} x = \frac{5}{4} \\ x = \frac{1}{8} \end{array} \end{array}$

$S = \{\frac{5}{4}; \frac{1}{8}\}$

Câu 6:

6.

x^{3} - 2 x^{2} + 2 - x = 0

Xem đáp án

$x^{3} - 2 x^{2} + 2 - x = 0$

$\begin{array}{l} \Leftrightarrow x^{2} (x - 2) - (x - 2) = 0 \\ \Leftrightarrow (x - 2) (x^{2} - 1) = 0 \\ \Leftrightarrow (x + 1) (x - 2) (x - 1) = 0 \\ \Leftrightarrow [\begin{array}{l} x + 1 = 0 \\ x - 2 = 0 \\ x - 1 = 0 \end{array} \Leftrightarrow [\begin{array}{l} x = - 1 \\ x = 2 \\ x = 1 \end{array} \end{array}$

Vậy, $S = \{- 1; 1; 2\}$

Câu 7:

7.

x^{2} - x - 12 = 0

Xem đáp án

$x^{2} - x - 12 = 0$

$\begin{array}{l} \Leftrightarrow x^{2} - 4 x + 3 x - 12 = 0 \\ \Leftrightarrow x (x - 4) + 3 (x - 4) = 0 \\ \Leftrightarrow (x - 4) (x + 3) = 0 \\ \Leftrightarrow [\begin{array}{l} x - 4 = 0 \\ x + 3 = 0 \end{array} \Leftrightarrow [\begin{array}{l} x = 4 \\ x = - 3 \end{array} \end{array}$

$S = \{- 3; 4\}$

Câu 8:

8 .

\frac{1}{x - 1} + \frac{2}{x + 1} = \frac{x}{x^{2} - 1}

Xem đáp án

$\frac{1}{x - 1} + \frac{2}{x + 1} = \frac{x}{x^{2} - 1}$ (ĐKXĐ: $x \neq \pm 1$ )

$\begin{array}{l} \Leftrightarrow \frac{x + 1 + 2 (x - 1)}{(x - 1) (x + 1)} = \frac{x}{x^{2} - 1} \\ \Leftrightarrow \frac{3 x - 1}{(x - 1) (x + 1)} = \frac{x}{(x - 1) (x + 1)} \\ \Rightarrow 3 x - 1 = x \\ \Leftrightarrow 2 x = 1 \\ \Leftrightarrow x = \frac{1}{2} (T M) \end{array}$

$S = \{\frac{1}{2}\}$

Câu 9:

9.

\frac{x + 5}{x - 5} - \frac{x - 5}{x + 5} = \frac{20}{x^{2} - 25}

Xem đáp án

$\frac{x + 5}{x - 5} - \frac{x - 5}{x + 5} = \frac{20}{x^{2} - 25}$ (ĐKXĐ: $x \neq \pm 5$ )

$\begin{array}{l} \Leftrightarrow \frac{{(x + 5)}^{2} - {(x - 5)}^{2}}{(x - 5) (x + 5)} = \frac{20}{(x - 5) (x + 5)} \\ \Leftrightarrow \frac{x^{2} + 10 x + 25 - x^{2} + 10 x - 25}{(x - 5) (x + 5)} = \frac{20}{(x - 5) (x + 5)} \\ \Leftrightarrow \frac{20 x}{(x - 5) (x + 5)} = \frac{20}{(x - 5) (x + 5)} \\ \Rightarrow 20 x = 20 \Leftrightarrow x = 1 (T M) \\ S = \{1\} \end{array}$

Câu 10:

10.

\frac{2}{x - 1} + \frac{4}{x + 3} = \frac{3 x + 11}{x^{2} + 2 x - 3}

Xem đáp án

$\frac{2}{x - 1} + \frac{4}{x + 3} = \frac{3 x + 11}{x^{2} + 2 x - 3}$ (ĐKXĐ: $x \neq 1, x \neq - 3$ )

$\begin{array}{l} \Leftrightarrow \frac{2 (x + 3) + 4 (x - 1)}{(x - 1) (x + 3)} = \frac{3 x + 11}{(x - 1) (x + 3)} \\ \Leftrightarrow \frac{2 x + 6 + 4 x - 4}{(x - 1) (x + 3)} = \frac{3 x + 11}{(x - 1) (x + 3)} \\ \Rightarrow 6 x + 2 = 3 x + 11 \\ \Leftrightarrow 3 x = 9 \\ \Leftrightarrow x = 3 (T M) \end{array}$

$S = \{3\}$

Câu 11:

Giải các phương trình sau

a. ${(2 x^{2} + 3 x - 1)}^{2} - 5. (2 x^{2} + 3 x + 3) + 24 = 0$

Xem đáp án

Đặt $2 x^{2} + 3 x = A$ ta có:

$\begin{array}{l} {(A - 1)}^{2} - 5. (A + 3) + 24 = 0 \\ \Leftrightarrow A^{2} - 7 A + 10 = 0 \\ \Leftrightarrow (A - 5) (A - 2) = 0 \\ \Rightarrow [\begin{array}{l} A - 5 = 0 \\ A - 2 = 0 \end{array} \Leftrightarrow [\begin{array}{l} A = 5 \\ A = 2 \end{array} \end{array}$

TH1: Với $A = 5 \Rightarrow 2 x^{2} + 3 x = 5$

$\begin{array}{l} \Leftrightarrow 2 x^{2} + 3 x - 5 = 0 \\ \Leftrightarrow (x - 1) (2 x + 5) = 0 \\ \Leftrightarrow [\begin{array}{l} x = 1 \\ x = \frac{- 5}{2} \end{array} \end{array}$

TH2: Với $A = 2 \Rightarrow 2 x^{2} + 3 x = 2$

$\begin{array}{l} \Leftrightarrow 2 x^{2} + 3 x - 2 = 0 \\ \Leftrightarrow (2 x - 1) (x + 2) = 0 \\ \Rightarrow [\begin{array}{l} x = \frac{1}{2} \\ x = - 2 \end{array} \end{array}$

$S = \{\frac{- 5}{2}; - 2; \frac{1}{2}; 1\}$

Câu 12:

b. $x^{3} - 3 x^{2} + 4 = 0$

Xem đáp án

$x^{3} - 3 x^{2} + 4 = 0$

$\begin{array}{l} \Leftrightarrow (x + 1) (x^{2} - 4 x + 4) = 0 \\ \Leftrightarrow (x + 1) {(x - 2)}^{2} = 0 \\ \Leftrightarrow [\begin{array}{l} x + 1 = 0 \\ {(x - 2)}^{2} = 0 \end{array} \Rightarrow [\begin{array}{l} x = - 1 \\ x = 2 \end{array} \end{array} S = \{- 1; 2\}$

Câu 13:

c.

x (x + 1) (x + 2) (x + 3) = 24

Xem đáp án

$x (x + 1) (x + 2) (x + 3) = 24$

$\begin{array}{l} \Leftrightarrow x . (x + 3) . (x + 1) . (x + 2) = 24 \\ \Leftrightarrow (x^{2} + 3 x) . (x^{2} + 3 x + 2) = 24 \end{array}$

Đặt $x^{2} + 3 x = A$ , ta có $A . (A + 2) = 24$

$\begin{array}{l} A^{2} + 2 A - 24 = 0 \\ \Leftrightarrow (A - 4) (A + 6) = 0 \\ \Leftrightarrow [\begin{array}{l} A - 4 = 0 \\ A + 6 = 0 \end{array} \Leftrightarrow [\begin{array}{l} A = 4 \\ A = - 6 \end{array} \end{array}$

TH1: $A = 4 \Rightarrow x^{2} + 3 x - 4 = 0$

$\begin{array}{l} \Leftrightarrow (x - 1) (x + 4) = 0 \\ \Leftrightarrow [\begin{array}{l} x - 1 = 0 \\ x + 4 = 0 \end{array} \Leftrightarrow [\begin{array}{l} x = 1 \\ x = - 4 \end{array} \end{array}$

TH2: $A = - 6 \Rightarrow x^{2} + 3 x + 6 = 0$

Ta có:

$x^{2} + 3 x + 6 = x^{2} + 2. \frac{3}{2} . x + \frac{9}{4} - \frac{9}{4} + 6 = {(x + \frac{3}{2})}^{2} + \frac{15}{4} > 0 \forall x \in ℝ$

=> không có giá trị nào của x thỏa mãn

x^{2} + 3 x + 6 = 0

Câu 14:

d.

\frac{x + 15}{60} + \frac{x + 14}{61} = \frac{x + 13}{62} + \frac{x + 12}{63}

Xem đáp án

$\frac{x + 15}{60} + \frac{x + 14}{61} = \frac{x + 13}{62} + \frac{x + 12}{63}$

$\begin{array}{l} \Leftrightarrow \frac{x + 15}{60} + 1 + \frac{x + 14}{61} + 1 = \frac{x + 13}{62} + 1 + \frac{x + 12}{63} + 1 \\ \Leftrightarrow \frac{x + 75}{60} + \frac{x + 75}{61} = \frac{x + 75}{62} + \frac{x + 75}{63} \\ \Leftrightarrow (x + 75) . (\frac{1}{60} + \frac{1}{61} - \frac{1}{62} - \frac{1}{63}) = 0 \end{array}$

Vì $\frac{1}{60} + \frac{1}{61} - \frac{1}{62} - \frac{1}{63} \neq 0 \Rightarrow x + 75 = 0 \Rightarrow x = - 75$

$S = \{- 75\}$

Câu 15:

e.

\frac{x + 9}{10} + \frac{x + 10}{9} = \frac{9}{x + 10} + \frac{10}{x + 9}

Xem đáp án

$\frac{x + 9}{10} + \frac{x + 10}{9} = \frac{9}{x + 10} + \frac{10}{x + 9}$ (ĐKXĐ: $x \neq - 9; x \neq - 10$ )

$\begin{array}{l} \Leftrightarrow \frac{x + 9}{10} + 1 + \frac{x + 10}{9} + 1 = \frac{9}{x + 10} + 1 + \frac{10}{x + 9} + 1 \\ \Leftrightarrow \frac{x + 19}{10} + \frac{x + 19}{9} = \frac{x + 19}{x + 10} + \frac{x + 19}{x + 9} \\ \Leftrightarrow (x + 19) . (\frac{1}{10} + \frac{1}{9} - \frac{1}{x + 10} - \frac{1}{x + 9}) = 0 \\ \Leftrightarrow [\begin{array}{l} x + 19 = 0 \\ \frac{1}{10} + \frac{1}{9} - \frac{1}{x + 10} - \frac{1}{x + 9} = 0 \end{array} \Leftrightarrow [\begin{array}{l} x = - 19 (T M) \\ x = 0 (T M) \end{array} \end{array} S = \{- 19; 0\}$

Câu 16:

Giải các phương trình sau:

a.

|2 x - 5| = 2 - x

Xem đáp án

$\begin{array}{l} d k : 2 - x \geq 0 \Leftrightarrow x \leq 2 \\ P T \Leftrightarrow [\begin{array}{l} 2 x - 5 = 2 - x \\ 2 x - 5 = - (2 - x) \end{array} \end{array}$ $\Leftrightarrow [\begin{array}{l} 3 x = 7 \\ x = 3 \end{array} \Leftrightarrow [\begin{array}{l} x = \frac{7}{3} \\ x = 3 \end{array} (l o ạ i)$

$S = \emptyset$

Câu 17:

b.

|3 x - 2| + x = 11

Xem đáp án

$|3 x - 2| + x = 11$ $\Leftrightarrow |3 x - 2| = 11 - x$

$\Leftrightarrow \begin{array}{l} D K : 11 - x \geq 0 \Leftrightarrow x \leq 11 \\ P T \Leftrightarrow [\begin{array}{l} 3 x - 2 = 11 - x \\ 3 x - 2 = - (11 - x) \end{array} \end{array} \Leftrightarrow [\begin{array}{l} 4 x = 13 \\ 2 x = - 9 \end{array} \Leftrightarrow [\begin{array}{l} x = \frac{13}{4} \\ x = \frac{- 9}{2} \end{array} (t m)$

$S = \{\frac{- 9}{2}; \frac{13}{4}\}$

Câu 18:

c.

|2 x - 1| = 1 - 2 x

Xem đáp án

$|2 x - 1| = 1 - 2 x$ $\Leftrightarrow |2 x - 1| = - (1 - 2 x) \Rightarrow 2 x - 1 \leq 0 \Leftrightarrow x \leq \frac{1}{2}$

Vậy: $S = \{x | x \leq \frac{1}{2}\}$

Câu 19:

d.

|- 4 x| = x^{2} + 4

Xem đáp án

$|- 4 x| = x^{2} + 4$

$\begin{array}{l} D K : x^{2} + 4 > 0 \forall x \in ℝ \\ P T \Leftrightarrow [\begin{array}{l} 4 x = x^{2} + 4 \\ 4 x = - (x^{2} + 4) \end{array} \Leftrightarrow [\begin{array}{l} x^{2} + 4 x + 4 = 0 \\ x^{2} - 4 x + 4 = 0 \end{array} \Leftrightarrow [\begin{array}{l} {(x + 2)}^{2} = 0 \\ {(x - 2)}^{2} = 0 \end{array} \Leftrightarrow [\begin{array}{l} x = - 2 \\ x = 2 \end{array} \end{array}$

$S = \{- 2; 2\}$

Câu 20:

Giải bất phương trình và biểu diễn tập nghiệm trên trục số:

a. $- 3 x + 6 \leq 0$

Xem đáp án

- 3 x + 6 \leq 0 \Leftrightarrow - 3 x \leq - 6 \Leftrightarrow x \geq - 6 : (- 3) \Leftrightarrow x \geq 2 . V ậ y : S = \{x |x \geq 2\}

Giải bất phương trình và biểu diễn tập nghiệm trên trục số: a. -3x + 6 nhỏ hơn bằng 0 (ảnh 1)

Câu 21:

b.

3 x + 4 < - 2 x - 3

Xem đáp án

3 x + 4 < - 2 x - 3

\Leftrightarrow 5 x < - 7 \Leftrightarrow x < \frac{- 7}{5} . V ậ y : S = \{x | x < \frac{- 7}{5}\}

Câu 22:

d.

\frac{2 x - 5}{3} > \frac{7 - x}{2}

Xem đáp án

\frac{2 x - 5}{3} > \frac{7 - x}{2}

\Leftrightarrow \frac{4 x - 10}{6} > \frac{21 - 3 x}{6} \Leftrightarrow 4 x - 10 > 21 - 3 x \Leftrightarrow 7 x > 31 \Leftrightarrow x > \frac{31}{7}

Vậy

S = \{x |x > \frac{31}{7}\}

Câu 23:

f. $\frac{x + 1}{4 x + 1} > 0$

Xem đáp án

\frac{x + 1}{4 x + 1} > 0

. ĐKXĐ:

x \neq - \frac{1}{4}

TH1:

\{\begin{cases} x + 1 > 0 \\ 4 x + 1 > 0 \end{cases} \Leftrightarrow \{\begin{cases} x > - 1 \\ 4 x > - 1 \end{cases} \Leftrightarrow \{\begin{cases} x > - 1 \\ x > - \frac{1}{4} \end{cases} \Leftrightarrow x > - \frac{1}{4}

Kết hợp đkxđ

\Rightarrow x > - \frac{1}{4}

TH2:

\{\begin{cases} x + 1 < 0 \\ 4 x + 1 < 0 \end{cases} \Leftrightarrow \{\begin{cases} x < - 1 \\ 4 x < - 1 \end{cases} \Leftrightarrow \{\begin{cases} x < - 1 \\ x < - \frac{1}{4} \end{cases} \Leftrightarrow x < - 1

Kết hợp đkxđ

\Rightarrow \{\begin{cases} x < - 1 \\ x \neq - \frac{1}{4} \end{cases} \Rightarrow x < - 1

Vậy

x < - 1

hoặc

x > - \frac{1}{4}

Câu 24:

Lúc 7 giờ một người đi xe máy khởi hành từ A với vận tốc 30km/h. Sau đó một giờ, người thứ hai cũng đi xe máy từ A đuổi theo với vận tốc 45km/h. Hỏi đến mấy giờ thì người thứ hai mới đuổi kịp người thứ nhất ? Nơi gặp nhau cách A bao nhiêu km ?

Xem đáp án

Gọi thời gian người thứ hai đi đến điểm gặp nhau là : x (h), (x > 0)

Khi đó : Thời gian người thứ nhất đi đến điểm gặp nhau là : x + 1 (h)

Quãng đường người thứ nhất đi là : 30 (x + 1) (km)

Quãng đường người thứ hai đi là : 54x (km)

Vì hai người cùng khởi hành từ A và gặp nhau tại một điểm nên ta có phương trình :

$30 (x + 1) = 45 x \begin{array}{l} \Leftrightarrow 30 x + 30 = 45 x \\ \Leftrightarrow x = 2 (T M) \end{array}$

Xe thứ hai gặp xe thứ nhất lúc : 2 + 1 + 7 = 10 ( giờ )

Nơi gặp nhau cách A : 2.45 = 90 (km)

Câu 25:

Một ô tô xuất phát từ A lúc 5 giờ và dự định đi đến B lúc 12 giờ cùng ngày. Ô tô đi hai phần ba đoạn đường đầu với vận tốc trung bình 40km/h. Để đến B đúng dự định, ô tô phải tăng vận tốc thêm 10km/h trên đoạn đường còn lại. Tính độ dài quãng đường AB

Xem đáp án

Gọi quãng đường AB $x (k m / h; x > 0)$

$\frac{2}{3}$ quãng đường AB là $\frac{2}{3} x$ (km)

Thời gian đi $\frac{2}{3}$ quãng đường AB là $\frac{2}{3} x : 40 = \frac{x}{60} (h)$

$\frac{1}{3}$ quãng đường còn lại là $\frac{2}{3} x$ (km)

Vận tốc ô tô đi trên quãng đường còn lại là $40 + 10 = 50 (k m / h)$

Thời gian đi $\frac{1}{3}$ quãng đường còn lại là $\frac{1}{3} x : 50 = \frac{x}{150} (h)$

Thời gian ô tô dự định đi từ A đến B là $12 - 5 = 7 (h)$

Theo đầu bài ta có phương trình:

$\begin{array}{l} \frac{x}{60} + \frac{x}{150} = 7 \\ \Leftrightarrow 5 x + 2 x = 2100 \\ \Leftrightarrow 7 x = 2100 \\ \Leftrightarrow x = 300 \begin{matrix} (T M) \end{matrix} \end{array}$

Vậy quãng đường AB dài 300km

Câu 26:

Một ca nô xuôi dòng từ bến A đến bến B mất 5 giờ và ngược dòng từ bến B về bến A mất 6 giờ. Tính khoảng cách giữa hai bến A và B, biết vận tốc dòng nước là 2km/h.

Xem đáp án

Gọi vân tốc riêng của ca nô là $x (k m / h; x > 2)$

Vận tốc của ca nô khi đi xuôi dòng là: $x + 2 (k m / h)$

Vận tốc của ca nô khi đi ngược dòng là $x - 2 (k m / h)$

Quãng đường ca nô xuôi dòng là $5 (x + 2) (k m)$

Quãng đường ca nô ngược dòng là $6 (x - 2) (k m)$

Theo đầu bài ta có phương trình:

$\begin{array}{l} 5 (x + 2) = 6 (x - 2) \\ \Leftrightarrow 5 x + 10 = 6 x - 12 \\ \Leftrightarrow x = 22 \begin{matrix} \end{matrix} (T M) \end{array}$

Vậy quãng đường AB dài là $5. (22 + 2) = 120 k m$

Câu 27:

Một xí nghiệp ký hợp đồng dệt một số tấm thảm len trong 16 ngày. Do cải tiến kĩ thuật, năng suất tăng 20% nên không những xí nghiệp đã hoan thành kế hoạch sớm 2 ngày mà còn dệt thêm được 24 tấm nữa. Tính số thảm len mà xí nghiệp phải dệt theo hợp đồng.

Xem đáp án

Gọi số thảm len mà xí nghiệp phải dệt theo hợp đồng trong một ngày là x (tấm/ ngày, $x \in N^{*}$ )

Số số thảm len mà xí nghiệp phải dệt theo hợp đồng là $16. x$ (tấm )

Do thực tế, năng suất tăng 20% nên năng suất thực tế của xí nghiệp là $120 % . x = 1, 2 x$ (tấm/ngày)

Vì hoàn thành sớm 2 ngày nên thời gian thực tế xí nghiệp làm là 16 - 2 =14 ( ngày)

Số thảm len thực tế xí nghiệp làm là 14.1,2x = 16,8x (tấm)

Do dệt thêm được 24 tấm nên ta có phương trình

$16, 8 x - 16 x = 24 \Leftrightarrow 0, 8 x = 24 \Leftrightarrow x = 30 (T M)$

Vậy số thảm len mà xí nghiệp phải dệt theo hợp đồng là 30.16 = 480 tấm.

Câu 28:

Một hình chữ nhật có chu vi 300cm. Nếu tăng chiều rộng thêm 5cm và giảm chiều dài đi 5cm thì diện tích hình chữ nhật đó tăng 275cm². Tính chiều dài và chiều rộng của hình chữ nhật.

Xem đáp án

Nửa chu vi hình chữ nhật là $\frac{300}{2} = 150 (c m)$

Gọi chiều dài hình chữ nhật là x ( $150 > x > 75$ , cm)

Chiều rộng hình chữ nhật là $150 - x$ (cm)

Diện tích hình chữ nhật ban đầu là $x . (150 - x) (c m^{2})$

Chiều dài sau khi giảm 5cm là : $x - 5 (c m)$

Chiều rộng sau khi tăng 5cm là $150 - x + 5 = 155 - x (c m)$

Diện tích hình chữ nhật mới là $(x - 5) (155 - x) (c m^{2})$

Vì diện tích tăng 275cm2 nên ta có phương trình

$\begin{array}{l} (x - 5) (155 - x) - x (150 - x) = 275 \\ \Leftrightarrow - x^{2} + 160 x - 755 - 150 x + x^{2} = 275 \\ \Leftrightarrow 10 x = 1030 \\ \Leftrightarrow x = 103 (T M) \end{array}$

Vậy chiều dài hình chữ nhật là 103 (cm)

Chiều rộng hình chữ nhật là $150 - 103 = 47 (c m)$