9 câu hỏi trắc nghiệm thuộc Đề kiểm tra 45 phút Toán 8 Chương 3 Đại Số có đáp án (Đề 2)

Top 12 Đề kiểm tra Toán 8 Học Kì 2 Chương 3 Đại Số có đáp án, cực hay

Đề kiểm tra 45 phút Toán 8 Chương 3 Đại Số có đáp án (Đề 2)

6736 lượt thi
9 câu hỏi
45 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

Phần trắc nghiệm (3 điểm)

Chọn câu có khẳng định đúng:

Phương trình có vô số nghiệm có tập nghiệm là:

A. S = R

B. S = ∅

C. S = {∅}

D. S = 0

Xem đáp án

Chọn A

Câu 2:

Chọn câu có khẳng định đúng: Chọn cặp phương trình tương đương.

A. $x = - 1 v à x (x + 1) = 0$

B. $5 x - 2 = 3 x + 4 v à 2 x = 2$

C. $5 (2 x + 3) = 0 v à 3 (2 x + 3) = 0$

D. $x^{2} - 4 = 0 v à x = 2$

Xem đáp án

Chọn C

Câu 3:

Phương trình $7 x + 49 = 0$ có tập nghiệm là:

A. S = {-4}

B. S = {-7}

C. S ={7}

D. S ={±7}

Xem đáp án

Chọn B

Câu 4:

Phương trình $2 x (x - 3) - 5 (x - 3) = 0$ có tập nghiệm là:

A. S = {0;3}

B. $S = \{3; \frac{5}{2}\}$

C. $S = \{3; - \frac{5}{2}\}$

D. $S = \{- 3; - \frac{5}{2}\}$

Xem đáp án

Chọn B

Câu 5:

Điều kiện xác định của phương trình: $\frac{x + 3}{x^{2} + 1} + \frac{x - 2}{x^{2} - 1} = 1$ là:

A. x ≠ -1

B. x ≠ 1

C. x ≠ ±1

D. x ≠ 0

Xem đáp án

Chọn C

Câu 6:

Chọn kết quả đúng: Cho biểu thức $M = \frac{2 x + 1}{x + 1} + \frac{x - 3}{x + 3}$ . Để M = 3 thì giá trị của x là:

A. $- \frac{9}{7}$

B. $- \frac{9}{17}$

C. $\frac{9}{7}$

D. $\frac{5}{7}$

Xem đáp án

Chọn A

Câu 7:

Phần tự luận (7 điểm)

a) Với giá trị nào của m thì hai phương trình sau tương đương?

$5 x - 3 = 7 x + 7 v à 5 x - m = 0$

b) Tìm m để phương trình sau có nghiệm x = 1 :

$3 (2 x + m) (x + 2) - 2 (2 x + 1) = 18 .$

Xem đáp án

a) Thay x = 1 vào phương trình đã cho, ta có :

3(2 + m)(1 + 2) – 2(2 + 1) = 18 ⇔ 18 + 9m – 6 = 18

⇔ m = 2/3

b) Ta có: 5x - 3 = 7x + 7 ⇔ 5x - 7x = 7 + 3 ⇔ -2x = 10 ⇔ x = -5

Vì phương trình 5x - 3 = 7x + 7 tương đương với phương trình 5x - m = 0 nên thay x = -5 vào phương trình 5x - m = 0 ta được:

5(-5) - m = 0 ⇔ -25 - m = 0 ⇔ m = -25

Vậy m = -25 thì hai phương trình đã cho tương đương.

Câu 8:

Giải các phương trình sau:

$a) {(5 x - 3)}^{2} = {(4 x - 7)}^{2} (*) b) \frac{96}{x^{2} - 16} + 6 = \frac{2 x - 1}{x + 4} + \frac{3 x - 1}{x - 4} c) \frac{1 - x}{2 x^{2} - 4 x} - \frac{1}{4 x - 4} = \frac{x - 1}{2 x (x - 2)} - \frac{1}{2 x}$

Xem đáp án

a) (*) ⇔ (5x – 3)2 – (4x – 7)2 = 0

⇔ (5x – 3 + 4x – 7)(5x – 3 – 4x + 7) = 0

⇔ (9x – 10)(x + 4) = 0 ⇔ 9x – 10 = 0 hoặc x + 4 = 0

⇔ x = 10/9 hoặc x = -4

Tập nghiệm : S = { 10/9 ; -4}

b) ĐKXĐ: (x + 4)(x – 4) ≠ 0 ⇔ x + 4 ≠ 0 và x – 4 ≠ 0 ⇔ x ≠ ⇔ 4

Ta có: x2 – 16 = (x + 4)(x – 4) ≠ 0

Quy đồng và khử mẫu, ta được:

96 + 6(x2 – 16) = (2x – 1)(x – 4) + (3x – 1)(x + 4)

⇔ 96 + 6x2 – 96 = 2x2 – 8x – x + 4 + 3x2 + 12x – x – 4

⇔ x2 – 2x = 0 ⇔ x(x – 2) = 0

⇔ x = 0 hoặc x – 2 = 0

⇔ x = 0 hoặc x = 2 (thỏa mãn ĐKXĐ)

Tập nghiệm: S = {0;2}

c) ĐKXĐ: x ≠ 0; x – 1 ≠ 0 và x – 2 ≠ 0 ⇔ x ≠ 0; x ≠ 1 và x ≠ 2

MTC: 4x(x – 2)(x – 1)

Quy đồng và khử mẫu, ta được:

2(1 – x)(x – 1) – x(x – 2) = 2(x – 1)2 – 2(x – 1)(x – 2)

⇔ -2x2 + 4x – 2 – x2 + 2x = 2x2 – 4x + 2 – 2x2 + 6x – 4

⇔ 3x2 – 4x = 0 ⇔ x(3x – 4) = 0 ⇔ x = 0 hoặc x = 4/3

(x = 0 không thỏa mãn ĐKXĐ)

Tập nghiệm: S = {4/3}

Câu 9:

Một người đi xe máy từ A đến B với vận tốc 30 km/h. Lúc về người đó đi với vận tốc 24 km/h nên thời gian về nhiều hơn thời gian đi là 30 phút. Tính quãng đường AB?

Xem đáp án

30 phút = (1/2) giờ

Gọi quãng đường AB là x (km). Điều kiện x > 0.

Thời gian xe máy đi từ A đến B là x/30 (giờ).

Thời gian xe máy đi từ B về A là x/24 (giờ).

Ta có phương trình:

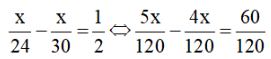
⇔ 5x - 4x = 60 ⇔ x = 60 (thỏa mãn điều kiện)

Vậy quãng đường AB là 60 km.

Bắt đầu thi ngay