Bài tập Toán 8 Chủ đề 1: Tam giác đồng dạng.Định lí Ta-Lét trong tam giác có đáp án
Dạng 1.Tính tỉ số hai đoạn thẳng. Chia đoạn thẳng theo tỉ số cho trước có đáp án
-
1568 lượt thi
-
6 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Điểm C thuộc đoạn thẳng AB và chia AB theo tỉ số . Hãy tính các tỉ số:.
 Xem đáp án
Xem đáp án
Vì C chia đoạn AB theo tỉ số nên:
Do đó . Vậy .
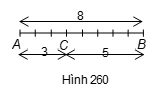
Câu 2:
Cho đoạn thẳng .Trên đoạn thẳng AB lấy điểm C sao cho . Tính độ dài CB.
![]()
 Xem đáp án
Xem đáp án
Cách 1: Từ giả thiết:
với ;
Nên . Vậy .
Cách 2: Từ giả thiết .
Vậy .
Cách 3: Đặt thì .
Từ giả thiết và tính chất cơ bản của tỉ lệ thức ta có hay
Câu 3:
Cho đoạn thẳng .Trên tia đối của tia BA lấy điểm D sao cho . Tính độ dài CD.
![]()
 Xem đáp án
Xem đáp án
Từ giả thiết .
Mặt khác D thuộc tia đối của tia BA nên .
Do đó , suy ra .
Vậy .
Câu 4:
Đoạn thẳng được chia thành các đoạn thẳng liên tiếp và PB lần lượt tỉ lệ với và 5. Tính độ dài mỗi đoạn thẳng đó.
 Xem đáp án
Xem đáp án
Từ giả thiết và tính chất của dãy tỉ số bằng nhau ta có:
.
Vậy .
Câu 5:
Đoạn thẳng AB=44dm được chia thành các đoạn thẳng liên tiếp và PB lần lượt tỉ lệ với và 5. Chứng minh rằng hai điểm M và P chia đoạn AN theo cùng một tỉ số k và tính k.
 Xem đáp án
Xem đáp án
Từ câu ta có .
Điều này chứng tỏ M và P chia đoạn AN theo cùng một tỉ số .
Câu 6:
Đoạn thẳng được chia thành các đoạn thẳng liên tiếp và PB lần lượt tỉ lệ với và 5. Còn hai điểm nào chia đoạn thẳng nào theo cùng một tỉ số nữa không?
 Xem đáp án
Xem đáp án
Vì ;
Nên còn hai điểm A và N chia đoạn MP theo cùng một tỉ số .
