9 câu hỏi trắc nghiệm thuộc Dạng 4. Tổng hợp có đáp án

Bài tập Toán 8 Chủ đề 14: Hình thoi có đáp án

Dạng 4. Tổng hợp có đáp án

947 lượt thi
9 câu hỏi
45 phút

Danh sách câu hỏi

Câu 1:

Cho tam giác ABC, phân giác AD. Qua D kẻ đường thẳng song song với AC cắt AB tại E, qua D kẻ đường thẳng song song với AB cắt AC tại F. Chứng minh EF là phân giác của

\hat{A E D} .

Xem đáp án

Chứng minh tứ giác AEDF là hình thoi

=> EF là phân giác của $\hat{A E D}$

Câu 2:

Cho hình chữ nhật ABCD. Gọi E, F, G, H lần lượt là trung điểm của AB, BC, CD, DA.

a) EFGH là hình gì? Vì sao?

Xem đáp án

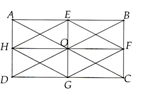
Cho hình chữ nhật ABCD. Gọi E, F, G, H lần lượt là trung điểm của AB, BC, CD, DA. a) EFGH là hình gì? Vì sao? (ảnh 1)

a) Áp dụng tính chất đường trung bình cho $△$ BAC và $△$ ADC ta có:

EF // HG; EF = HG = $\frac{1}{2}$ AC và HE // HG; HE = FG = $\frac{1}{2}$ BD.

Mà ABCD là hình chữ nhật nên AB = BD => EFGH là hình thoi.

Câu 3:

b) Chứng minh AC, BD, EG, FH đồng qui.

Xem đáp án

b) Gọi O = AC $\cap$ BD => O là trung điểm của AC và BD. Chứng minh EBGD và BFDH là hình bình hành suy ra AC, BD,EG, FH đồng quy tại trung điểm mỗi đường (điểm O).

Câu 4:

b) Chứng minh PQ // BC.

Xem đáp án

b) Vì PQ $⊥$ AM mà AM $⊥$ BC (tính chất tam giác cân) nên PQ // BC.

Câu 5:

Cho hình bình hành ABCD. Trên các cạnh AB và CD lần lượt lấy các điểm M và N sao cho AM = DN. Đường trung trực của BM lần lượt cắt các đường thẳng MN và BC tại E và F.

a) Chứng minh E và F đối xứng với nhau qua AB.

Xem đáp án

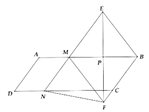
Cho hình bình hành ABCD. Trên các cạnh AB và CD lần lượt lấy các điểm M và N a) Chứng minh E và F đối xứng với nhau qua AB. (ảnh 1)

a) Do AM = DN => MADN là hình bình hành

$\Rightarrow \hat{D} = \hat{A M N} = \hat{E M B} = \hat{M B C}$

Ta có $△$ MPE = $△$ BPE nên EP = FP. Vậy MEBF là hình thoi và 2 điểm E, F đối xứng nhau qua AB.

Câu 6:

b) Chứng minh tứ giác MEBF là hình thoi

Xem đáp án

b) Tứ giác MEBF có MB $\cap$ EF = P; Lại có P trung điểm BM, P là trung điểm EF, MB $⊥$ EF.

=> MEBF là hình thoi.

Câu 7:

c) Hình bình hành ABCD có thêm điều kiện gì để tứ giác BCNE là hình thang cân.

Xem đáp án

c) Để BNCE là hình thang cân thì $\hat{C N E} = \hat{B E N}$

Mà $\hat{C N E} = \hat{D} = \hat{M B C} = \hat{E B M}$ nên $△$ MEB có 3 góc bằng nhau, suy ra điều kiện để BNCE là hình thang cân thì $\hat{A B C} = 60^{0}$

Câu 8:

Cho tam giác ABC nhọn, các đường cao BD, CE. Tia phân giác của các góc $\hat{A B D}$ và $\hat{A C E}$ cắt nhau tại O, và lần lượt cắt AC, AB tại N, M. Tia BN cắt CE tại K, tia CM cắt BD tại H: Chứng minh rằng:

a) BN $⊥$ CM;

Xem đáp án

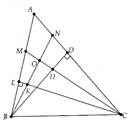
Cho tam giác ABC nhọn, các đường cao BD, CE. Tia phân giác của các góc ABD và ACE cắt nhau tại O, Chứng minh rằng: a) BN CM; (ảnh 1)

a) Sử dụng tính chất tổng các góc trong một tam giác bằng 180^o.

$\Rightarrow \hat{A B C} = \hat{A E C} \Rightarrow \hat{N B D} = \hat{M C A}$

Trong $△$ DBN có: $\hat{N B D} + \hat{B N D} = 90^{0}$

Gọi O = CM $\cap$ BN => CM $⊥$ BN = O (1)

Câu 9:

b) Tứ giác MNFIK là hình thoi.

Xem đáp án

b) Xét $△$ CNK có: CO ^ KN => CO $⊥$ BN, CO là phân giác $\hat{A C E}$ nên $△$ CNK cân ở C => O là trung điểm KN (2).

Tương tự chứng minh được là trung điểm MH (3).

Từ (1),(2) và (3) suy ra MNHK là hình thoi.

Bắt đầu thi ngay