5 câu hỏi trắc nghiệm thuộc Đề kiểm tra giữa kỳ 2 Toán 8 có đáp án ( Mới nhất)_ đề số 4

Câu 1:

Cho biểu thức:

$P = (\frac{x^{2} + 1}{x^{2} - 9} - \frac{x}{x + 3} + \frac{5}{3 - x}) : (\frac{2 x + 10}{x + 3} - 1)$ với x ≠ 3, x ≠ −3, x ≠ −7.

a) Rút gọn P.

b) Tính P khi |x – 1| = 2.

c) Tìm x để $P = \frac{x + 5}{6}$ .

Xem đáp án

a) Rút gọn P. Với x ≠ 3, x ≠ −3, x ≠ −7.

$P = (\frac{x^{2} + 1}{x^{2} - 9} - \frac{x}{x + 3} + \frac{5}{3 - x}) : (\frac{2 x + 10}{x + 3} - 1)$

$= [\frac{x^{2} + 1}{(x + 3) (x - 3)} - \frac{x}{x + 3} - \frac{5}{x - 3}] : (\frac{2 x + 10}{x + 3} - \frac{x + 3}{x + 3})$

$= [\frac{x^{2} + 1}{(x + 3) (x - 3)} - \frac{x (x - 3)}{(x + 3) (x - 3)} - \frac{5 (x + 3)}{(x + 3) (x - 3)}] : (\frac{2 x + 10}{x + 3} - \frac{x + 3}{x + 3})$

$= \frac{x^{2} + 1 - x (x - 3) - 5 (x + 3)}{(x + 3) (x - 3)} : \frac{2 x + 10 - (x + 3)}{x + 3}$

$= \frac{x^{2} + 1 - x^{2} + 3 x - 5 x - 15}{(x + 3) (x - 3)} : \frac{x + 7}{x + 3}$

$= \frac{- 2 x - 14}{(x + 3) (x - 3)} . \frac{x + 3}{x + 7}$ $= \frac{- 2}{x - 3}$

b) Ta có |x – 1| = 2.

$\Leftrightarrow$ x – 1 = 2 hoặc x – 1 = – 2

$\Leftrightarrow$ x = 3 (loại) hoặc x = – 1 (TM).

Thay x = – 1 vào $P = \frac{- 2}{x - 3}$ , ta được:

$P = \frac{- 2}{- 1 - 3} = \frac{- 2}{- 4} = \frac{1}{2}$ .

c) Ta có $P = \frac{x + 5}{6} \Leftrightarrow \frac{- 2}{x - 3} = \frac{x + 5}{6}$

$\Leftrightarrow$ (x – 3)(x + 5) = −12

$\Leftrightarrow$ x² + 2x – 15 = −12

$\Leftrightarrow$ x² + 2x – 3 = 0

$\Leftrightarrow$ x² – x + 3x – 3 = 0

$\Leftrightarrow$ x(x – 1) + 3(x – 1) = 0

$\Leftrightarrow$ (x – 1)(x + 3) = 0

$\Leftrightarrow$ x – 1 = 0 hoặc x + 3 = 0

$\Leftrightarrow$ x = 1 (TM) hoặc x = – 3 (loại).

Vậy để $P = \frac{x + 5}{6}$ thì x = – 1.

Câu 2:

Lúc 6 giờ sáng một ô tô khởi thành từ A để đi đến B. Đến 7 giờ 30 phút một ô tô thứ hai cũng khởi hành từ A để đi đến B với vận tốc lớn hơn vận tốc ô tô thứ nhất là 20km/h và hai xe gặp nhau lúc 10 giờ 30 phút. Tính vận tốc mỗi ô tô? (ô tô không bị hư hỏng hay dừng lại dọc đường).

Xem đáp án

Gọi vận tốc của ô tô thứ nhất là x (km/h) (ĐK: x > 0)

Vận tốc của ô tô thứ hai lớn hơn vận tốc của ô tô thứ nhất là 20km/h, nên vận tốc của ô tô thứ hai là: x + 20 (km/h).

Đến khi hai xe gặp nhau (lúc 10 giờ 30 phút):

- Thời gian đi của ô tô thứ nhất là:

10 giờ 30 phút – 6 giờ = 4 giờ 30 phút = $\frac{9}{2}$ giờ.

- Thời gian đi của ô tô thứ hai là:

10 giờ 30 phút – 7 giờ 30 phút = 3 giờ.

Khi đó, quãng đường ô tô thứ nhất đi được: $\frac{9}{2} x$ (km)

Quãng đường ô tô thứ hai đi được: 3(x + 20) (km).

Theo đề bài, ta có phương trình: $\frac{9}{2} x = 3 (x + 20)$

$\Leftrightarrow \frac{9}{2} x - 3 x = 60$

$\Leftrightarrow \frac{3}{2} x = 60$

$\Leftrightarrow$ x = 40 (TMĐK).

Vậy vận tốc của ô tô thứ nhất là 40 (km/h);

Vận tốc của ô tô thứ hai là 40 + 20 = 60 (km/h).

Câu 3:

Giải các phương trình sau:

a) 9x² – 3 = (3x + 1)(2x – 3)

b) $\frac{3 x}{x - 5} + \frac{1}{x} = \frac{4 x + 3}{x (x - 5)} + 3$

Xem đáp án

a) 9x² – 3 = (3x + 1)(2x – 3)

$\Leftrightarrow$ 9x² – 3 = 6x² – 7x – 3

$\Leftrightarrow$ 3x² – 7x = 0

$\Leftrightarrow$ x(3x – 7) = 0

$\Leftrightarrow$ x = 0 hoặc 3x – 7 = 0

$\Leftrightarrow$ x = 0 hoặc $x = \frac{7}{3}$ .

Vậy tập nghiệm của phương trình đã cho là $S = {0; \frac{7}{3}}$ .

b) $\frac{3 x}{x - 5} + \frac{1}{x} = \frac{4 x + 3}{x (x - 5)} + 3$ .

ĐK: x ≠ 0; x ≠ 5.

Phương trình đã cho tương đương:

$\frac{3 x^{2}}{x (x - 5)} + \frac{x - 5}{x (x - 5)} = \frac{4 x + 3}{x (x - 5)} + \frac{3 x (x - 5)}{x (x - 5)}$

$\Leftrightarrow$ 3x² + x – 5 = 4x + 3 + 3x(x – 5)

$\Leftrightarrow$ 3x² + x – 5 = 4x + 3 + 3x² – 15x

$\Leftrightarrow$ x – 5 = 4x + 3 – 15x

$\Leftrightarrow$ 12x = 8

$\Leftrightarrow x = \frac{2}{3}$ (TMĐK).

Vậy tập nghiệm của phương trình đã cho là $S = {\frac{2}{3}}$ .

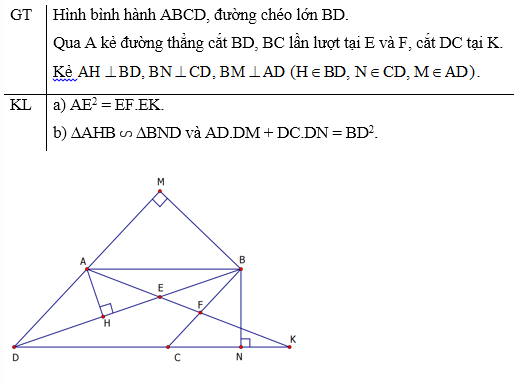
Câu 4:

Cho hình bình hành ABCD, đường chéo lớn BD. Qua A kẻ đường thẳng cắt các đoạn thẳng BD, BC lần lượt tại E và F, cắt DC tại K.

a) Chứng minh AE² = EF.EK.

b) Kẻ $A H ⊥ B D, B N ⊥ C D, B M ⊥ A D$ $(H \in B D, N \in C D, M \in A D)$ .

Chứng minh: ∆AHB đồng dạng với ∆BND và AD.DM + DC.DN = BD².

Xem đáp án

Vì ABCD là hình bình hành nên:

+ AD // BC hay AD // BF

+ AB // CD hay AB // DK.

Áp dụng định lý Ta-let, ta có:

+ AD // BF suy ra: $\frac{A E}{E F} = \frac{E D}{E B}$ (1)

+ AB // DK suy ra: $\frac{E D}{E B} = \frac{E K}{A E}$ (2)

Từ (1) và (2) suy ra: $\frac{A E}{E F} = \frac{E K}{A E}$ .

Do đó AE² = EF.EK (đpcm).

b) Xét ∆AHB và ∆BND có:

$\hat{A H B} = \hat{B N D} = 90^{o}$

$\hat{A B H} = \hat{B D N}$ (AB // DK, hai góc so le trong)

Do đó ∆AHB ∆BND (g.g) (đpcm)

Suy ra $\frac{A B}{B D} = \frac{B H}{D N} \frac{A B}{B D} = \frac{B H}{D N}$ $\Leftrightarrow$ AB.DN = BD.BH

Mà AB = DC nên DC.DN = BD.BH (1)

Xét ∆ADH và ∆BDM có:

$\hat{A H D} = \hat{B M D} = 90^{o}$

$\hat{B D M}$ chung.

Do đó ∆ADH ∆BDM (g.g).

Suy ra $\frac{A D}{D B} = \frac{D H}{D M}$ $\Leftrightarrow$ AD.DM = DH.DB (2)

Từ (1) và (2) suy ra: AD.DM + DC.DN = BD.BH + DH.DB = BD.(BH + HD)

= BD.BD = BD².

Do đó AD.DM + DC.DN = BD² (đpcm).

Câu 5:

Cho a, b, c đôi một khác nhau và $\frac{1}{a} + \frac{1}{b} + \frac{1}{c} = 0$ . Tính giá trị biểu thức: $P = \frac{1}{a^{2} + 2 b c} + \frac{1}{b^{2} + 2 a c} + \frac{1}{c^{2} + 2 a b}$ .

Xem đáp án

Ta có $\frac{1}{a} + \frac{1}{b} + \frac{1}{c} = 0 \Rightarrow \frac{a b + b c + c a}{a b c} = 0$ $\Rightarrow$ ab + bc + ca = 0.

Ta thấy a² + 2bc = a² + bc + (–ab – ac) = a(a – b) – c(a – b) = (a – b)(a – c)

Tương tự, b² + 2ac = (b – a)(b – c)

c² + 2ab = (c – a)(c – b).

Khi đó, $P = \frac{1}{a^{2} + 2 b c} + \frac{1}{b^{2} + 2 a c} + \frac{1}{c^{2} + 2 a b}$

$= \frac{1}{(a - b) (a - c)} + \frac{1}{(b - a) (b - c)} + \frac{1}{(c - a) (c - b)}$

$= \frac{b - c + c - a + a - b}{(a - b) (b - c) (a - c)} = 0$ .

Vậy $P = \frac{1}{a^{2} + 2 b c} + \frac{1}{b^{2} + 2 a c} + \frac{1}{c^{2} + 2 a b} = 0$ .