23 câu hỏi trắc nghiệm thuộc Đề kiểm tra cuối kỳ 2 Toán 8 có đáp án ( Mới nhất)_ đề 13

Câu 1:

Giá trị x = - 4 là nghiệm của phương trình nào sau đây?

A. -2x = -8;

B. -2x = 8;

C. 2x - 8 = 0;

D. 3x - 1 = x + 7.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: B

+) -2x = -8 Û x = 4

Do đó x = 4 là nghiệm của phương trình -2x = -8.

+) -2x = 8 Û x = -4

Do đó x = -4 là nghiệm của phương trình -2x = 8.

+) 2x - 8 = 0 Û 2x = 8 Û x = 4

Do đó x = 4 là nghiệm của phương trình 2x - 8 = 0

+) 3x - 1 = x + 7

Û 3x - x = 7 + 1

Û 2x = 8 Û x = 4

Do đó x = 4 là nghiệm của phương trình 3x - 1 = x + 7.

Câu 2:

Phương trình x - 2 = 5 tương đương với phương trình

A. 2x = 14;

B. (x - 2)x = 5;

C. |x - 2| = 5;

D. (x - 2)² = 25.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: A

Hai phương trình tương đương là hai phương trình có chung tập nghiệm

Ta có: x - 2 = 5 Û x = 7.

Vậy phương trình tương đương với phương trình trên là phương trình cho một nghiệm duy nhất là x = 7

+) 2x = 14 Û x = 7

Vậy phương trình 2x = 14 tương đương với phương trình đã cho.

+) (x - 2)x = 5

Û x² - 2x + 1 = 6

Û (x - 1)² = 6

$\Leftrightarrow [\begin{matrix} x - 1 = \sqrt{6} \\ x - 1 = - \sqrt{6} \end{matrix}$

$\Leftrightarrow [\begin{matrix} x = 1 + \sqrt{6} \\ x = 1 - \sqrt{6} \end{matrix}$

Do đó phương trình (x - 2)x = 5 không tương đương với phương trình đã cho.

+) |x - 2| = 5

$\Leftrightarrow [\begin{matrix} x - 2 = 5 \\ x - 2 = - 5 \end{matrix}$

$\Leftrightarrow [\begin{matrix} x = 7 \\ x = - 3 \end{matrix}$

Do đó phương trình |x - 2| = 5 không tương đương với phương trình đã cho.

+) (x - 2)² = 25

$\Leftrightarrow [\begin{matrix} x - 2 = 5 \\ x - 2 = - 5 \end{matrix}$

$\Leftrightarrow [\begin{matrix} x = 7 \\ x = - 3 \end{matrix}$

Do đó phương trình không tương đương với phương trình đã cho.

Câu 3:

Cho a < b. Khẳng định nào sau đây đúng?

A. -2a < -2b;

B. -2a > -2b;

C. a - 1 > b - 1;

D. a + 2 > b + 2.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: B

∙ a < b Þ -2a > -2b

∙ a < b Þ a - 1 < b - 1

∙ a < b Þ a - 1 < b - 1.

Câu 4:

Hình vẽ sau biểu diễn tập nghiệm của bất phương trình nào?

A. x ³ 5;

B. x > 5;

C. x £ 5;

D. x < 5.

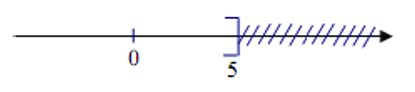
Xem đáp án

Hướng dẫn giải

Đáp án đúng là: C

Dựa vào hình vẽ ta thấy x £ 5.

Vậy hình vẽ sau biểu diễn tập nghiệm của bất phương trình x £ 5.

Câu 5:

Tập nghiệm của phương trình (x² + 1)(x - 2) = 0 là

A. S = {-1; -2};

B. S = {-1; 2};

C. S = {-1};

D. S = {2}.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: D

(x² + 1)(x - 2) = 0

Þ x - 2 = 0 (do x² + 1 > 0 "x Î ℝ)

Û x = 2

Vậy tập nghiệm của phương trình là S = {2}.

Câu 6:

Số nghiệm của phương trình |x + 1| + 1 = 0 là

A. 0;

B. 1;

C. 2;

D. 3.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: A

Phương trình |x + 1| + 1 = 0

Vì |x + 1| ³ 0 "x Î ℝ nên |x + 1| + 1 ³ 1 "x Î ℝ

Vậy phương trình đã cho không cho nghiệm.

Câu 7:

Điều kiện xác định của phương trình $\frac{x}{x^{2} - 1} = \frac{1}{x - 1}$ là

A. x ¹ 1;

B. x ¹ ± 1;

C. x ¹ 0;

D. x ¹ -1.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: B

$\frac{x}{x^{2} - 1} = \frac{1}{x - 1}$

$\Leftrightarrow \frac{x}{(x - 1) (x + 1)} = \frac{1}{x - 1}$

ĐKXĐ: $\{\begin{matrix} x - 1 \neq 0 \\ x + 1 \neq 0 \end{matrix} \Leftrightarrow \{\begin{matrix} x \neq 1 \\ x \neq - 1 \end{matrix}$

Vậy điều kiện xác định của phương trình $\frac{x}{x^{2} - 1} = \frac{1}{x - 1}$ là x ¹ ± 1.

Câu 8:

An có 60 000 đồng, An mua bút hết 15 000 đồng, còn lại An mua vở với giá mỗi quyển vở là 6 000 đồng. Số quyển vở An có thể mua nhiều nhất là

A. 7 quyển;

B. 8 quyển;

C. 9 quyển;

D. 10 quyển.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: A

Sau khi mua bút, số tiền còn lại của An là:

60 000 - 15 000 = 45 000 (đồng).

Ta có: $\frac{45 000}{6 000} = 7,5$ .

Với giá mỗi quyển vở là 6 000 đồng thi An mua được 7 quyển vở và dư 3 000 đồng.

Vậy với giá mỗi quyển vở là 6 000 đồng thì An mua được nhiều nhất 7 quyển vở.

Câu 9:

Cho DABC có MN // BC (với M Î AB; N Î AC). Khi đó

A. $\frac{A M}{A B} = \frac{A C}{A N};$

B. $\frac{A M}{A B} = \frac{A N}{B C};$

C. $\frac{A M}{A B} = \frac{A N}{A C};$

D. $\frac{A M}{A B} = \frac{B C}{M N} .$

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: C

Theo đề bài DABC có MN // BC (với M Î AB; N Î AC).

Áp dụng định lý Ta-lét ta có:

$\frac{A M}{A B} = \frac{A N}{A C} .$

Câu 10:

Cho ∆ABC ᔕ ∆MNP với tỉ số đồng dạng là $\frac{3}{5}$ . Khi đó tỉ số chu vi của DABC và DMNP là

A. $\frac{9}{25};$

B. $\frac{25}{9}$

C. $\frac{5}{3}$

D. $\frac{3}{5}$

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: D

Hai tam giác ∆ABC và ∆MNP đồng dạng với tỉ số là $\frac{3}{5}$ . Khi đó:

$\frac{A B}{M N} = \frac{B C}{N P} = \frac{A C}{M P} = \frac{3}{5}$

$\Rightarrow \{\begin{matrix} A B = \frac{3}{5} M N \\ B C = \frac{3}{5} N P \\ A C = \frac{3}{5} M P \end{matrix}$

Vậy suy ra tỉ số chu vi của DABC và DMNP là

$\frac{C_{A B C}}{C_{M N P}} = \frac{A B + B C + A C}{M N + N P + M P}$

$= \frac{\frac{3}{5} M N + \frac{3}{5} N P + \frac{3}{5} M P}{M N + N P + M P}$

$= \frac{\frac{3}{5} (M N + N P + M P)}{M N + N P + M P} = \frac{3}{5} .$

Câu 11:

Cho DABC vuông tại A, có AB = 3cm, BC = 5cm. Tia phân giác của $\hat{A}$ cắt BC tại E thì $\frac{E B}{E C}$ bằng

A. $\frac{5}{3}$

B. $\frac{3}{5}$

C. $\frac{3}{4}$

D. $\frac{4}{3}$

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: C

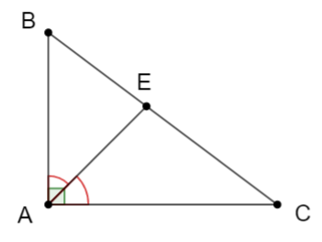
Cho tam giác ABC vuông tại A, có AB = 3cm, BC = 5cm. Tia phân giác của góc A cắt BC tại E thì EB/EC bằng (ảnh 1)

Áp dụng định lý Py-ta-go vào tam giác ABC vuông tại A có:

$A C = \sqrt{B C^{2} - A B^{2}} = \sqrt{5^{2} - 3^{2}} = 4 (c m)$

Sử dụng tính chất đường phân giác vào tam giác ABC có AE là đường phân giác trong ta có:

$\frac{B E}{E C} = \frac{A B}{A C} = \frac{3}{4} .$

Câu 12:

Hình hộp chữ nhật ABCD.A’B’C’D’ có AB = 3cm; BC = 5cm; AA’ = 4cm (hình vẽ). Khi đó thể tích của hình hộp chữ nhật là

A. 60 cm;

B. 60 cm²;

C. 60 cm³;

D. 6 dm³.

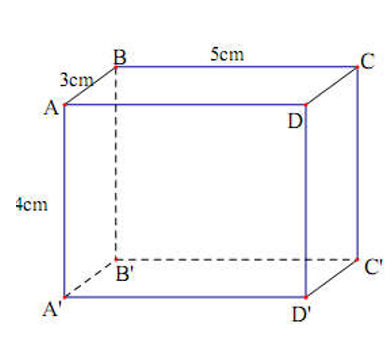
Xem đáp án

Hướng dẫn giải

Đáp án đúng là: C

Áp dụng công thức tính thể tích hình hộp chữ nhật ta có:

$V_{A B C D . A' B' C' D'} = A B . B C . A A' = 3.5.4 = 60 (c m^{3}) .$

Câu 13:

Giải các phương trình và bất phương trình sau:

a) -7x + 21 = 0.

Xem đáp án

Hướng dẫn giải

a) -7x + 21 = 0

Û 7x = 21

Û x = 3

Vậy tập nghiệm của phương trình là S = {3}.

Câu 14:

Giải các phương trình và bất phương trình sau:

b) 3x + 2 > 8.

Xem đáp án

b) 3x + 2 > 8

Û 3x > 8 - 2

Û 3x > 6 Û x > 2

Vậy tập nghiệm của bất phương trình là S = {x | x > 2}.

Câu 15:

Giải các phương trình và bất phương trình sau:

c) $\frac{x + 3}{x + 1} - \frac{x - 1}{x} = \frac{x^{2} + 5 x + 1}{x (x + 1)} .$

Xem đáp án

c)

$\frac{x + 3}{x + 1} - \frac{x - 1}{x} = \frac{x^{2} + 5 x + 1}{x (x + 1)}$

ĐKXĐ: $\{\begin{matrix} x \neq 0 \\ x + 1 \neq 0 \end{matrix} \Leftrightarrow \{\begin{matrix} x \neq 0 \\ x \neq - 1 \end{matrix}$

$\Leftrightarrow \frac{x (x + 3)}{x (x + 1)} - \frac{(x - 1) (x + 1)}{x (x + 1)} = \frac{x^{2} + 5 x + 1}{x (x + 1)}$

$\Leftrightarrow \frac{x^{2} + 3 x}{x (x + 1)} - \frac{x^{2} - 1}{x (x + 1)} = \frac{x^{2} + 5 x + 1}{x (x + 1)}$

$\Leftrightarrow \frac{x^{2} + 3 x - x^{2} + 1}{x (x + 1)} = \frac{x^{2} + 5 x + 1}{x (x + 1)}$

$\Leftrightarrow \frac{3 x + 1}{x (x + 1)} = \frac{x^{2} + 5 x + 1}{x (x + 1)}$

Þ 3x + 1 = x² + 5x + 1

Û x² + 2x = 0

Û x(x + 2) = 0

$\Rightarrow [\begin{matrix} x = 0 \\ x + 2 = 0 \end{matrix} \Leftrightarrow [\begin{matrix} x = 0 \\ x = - 2 \end{matrix}$

Đối chiếu ĐKXĐ suy ra x = -2 là nghiệm của phương trình.

Câu 16:

Một ô tô đi từ A đến B với vận tốc 50 km/h, rồi đi từ B về A với vận tốc lớn hơn vận tốc lúc đi là 10 km/h. Tính quãng đường AB, biết thời gian về ít hơn thời gian đi là 24 phút.

Xem đáp án

Hướng dẫn giải

Gọi x (km) là độ dài quãng đường AB.

Thời gian ô tô đi từ A đến B với vận tốc 50 km/h là $\frac{x}{50}$ (h)

Ô tô đi từ B về A với vận tốc lớn hơn lúc đi 10 km/h tức là 60 km/h với số thời gian là $\frac{x}{60}$ (h)

Đổi 24 phút = $\frac{2}{5}$ giờ.

Do thời gian về ít hơn thời gian đi là 24 phút nên ta có phương trình:

$\frac{x}{50} - \frac{x}{60} = \frac{2}{5}$

$\Leftrightarrow \frac{6 x}{300} - \frac{5 x}{300} = \frac{2}{5}$

$\Leftrightarrow \frac{x}{300} = \frac{2}{5}$

$\Leftrightarrow x = 300. \frac{2}{5} = 120$ (thỏa mãn)

Vậy quãng đường AB dài 200 km.

Câu 17:

Cửa hàng đồng giá 50 000 đồng một món, có chương trình giảm giá 10% cho một món hàng. Nếu khách hàng mua 3 món trở lên thì từ món thứ 3 trở đi khách hàng chỉ phải trả 70% giá đang bán.

a) Tính số tiền một khách hàng phải trả khi mua 8 món hàng.

Xem đáp án

Hướng dẫn giải

a) Số tiền một khách hàng phải trả khi mua 8 món hàng là:

50 000.(100% − 10%).2 + 50 000.70%.6

= 50 000.0,9.2 + 50 000.0,7.6

= 90 000 + 210 000 = 300 000 (đồng)

Câu 18:

b) Nếu có khách hàng đã trả 475 000 đồng thì khách hàng này đã mua bao nhiêu món hàng?

Xem đáp án

b) Số món hàng đã mua nếu khách hàng đã trả 475 000 đồng.

Với 300 000 đồng, khách hàng đã mua 8 món hàng.

Với số tiền 475 000 > 300 000 thì khách hàng mua thêm được:

(475 000 – 300 000) : (50 000.70%)

= 175 000 : (50 000.0,7)

= 175 000 : 35 000 = 5 (món)

Người đó đã mua: 5 + 8 = 13 (món hàng).

Vậy người đó đã mua 13 món hàng.

Câu 19:

Cho DABC vuông tại A có đường cao AH.

a) Chứng minh ∆HAC ᔕ ∆ABC.

Xem đáp án

Hướng dẫn giải

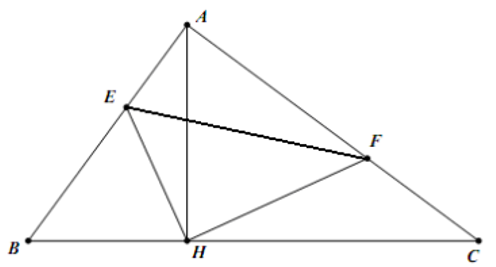
Cho ABC vuông tại A có đường cao AH. a) Chứng minh ∆HAC ᔕ ∆ABC. (ảnh 1)

a) Xét hai tam giác HAC và ABC ta có

$\begin{matrix} \hat{A H C} = \hat{B A C} (= 90 °) \\ \hat{H C A} = \hat{A C B} (\hat{B} c h u n g) \end{matrix}\} \Rightarrow Δ H A C ∽ Δ A B C (g . g) .$

Câu 20:

b) Tính độ dài đoạn thẳng AC, biết CH = 4cm; BC = 13cm.

Xem đáp án

b) ∆HAC ᔕ ∆ABC

$\Rightarrow \frac{H C}{A C} = \frac{A C}{B C} \Leftrightarrow A C^{2} = H C . B C$

$\Rightarrow A C = \sqrt{H C . B C} = \sqrt{4.13} = 2 \sqrt{13} c m .$

Câu 21:

c) Gọi E là điểm tùy ý trên cạnh AB, đường thẳng qua H và vuông góc với HE cắt cạnh AC tại F. Chứng minh AE.CH = AH.FC.

Xem đáp án

c) Xét DEHA và DFHC, ta có:

+) $\hat{E H A} + \hat{A H F} = \hat{E H F} = 90 °$ (1)

+) $\hat{F H C} + \hat{A H F} = \hat{A H C} = 90 °$ (2)

Từ (1) và (2) nên suy ra $\hat{E H A} = \hat{H F C} = 90 ° - \hat{A H F}$ (5)

Lại có:

+) $\hat{E A H} + \hat{H A F} = \hat{E A F} = 90 °$ (3)

+) $\hat{H C F} + \hat{H A F} = 180 ° - 90 ° = 90 °$ (4)

Từ (3) và (4) nên suy ra $\hat{E A H} = \hat{H C F} = 90 ° - \hat{H A F}$ (6)

Từ (5) và (6) nên suy ra ∆EHA ᔕ ∆FHC (g.g)

$\Rightarrow \frac{A E}{C F} = \frac{H A}{H C} \Leftrightarrow A E . C H = A H . F C$ (đpcm).

Câu 22:

d) Tìm vị trí của điểm E trên cạnh AB để tam giác HEF có diện tích nhỏ nhất.

Xem đáp án

d) Ta có:

+) ∆EHA ᔕ ∆FHC (cmt)

$\Rightarrow \frac{E H}{F H} = \frac{H A}{H C}$

+) ∆HAC ᔕ ∆ABC (cmt)

$\Rightarrow \frac{A B}{A C} = \frac{H A}{H C}$

Suy ra $\frac{E H}{F H} = \frac{A B}{A C} (= \frac{H A}{H C})$

$\Leftrightarrow \frac{H E}{A B} = \frac{H F}{A C}$

+) Xét DEHF và DBAC có:

$\begin{matrix} \frac{H E}{A B} = \frac{H F}{A C} (c m t) \\ \hat{E H F} = \hat{B A C} (= 90 °) \end{matrix}\} \Rightarrow Δ E H F ∽ Δ B A C (c . g . c)$

Khi đó tỉ lệ diện tích của hai tam giác DEHF và DBAC cũng bằng bình phương tỉ lệ của hai cạnh HE và AB

$\Leftrightarrow \frac{S_{E H F}}{S_{B A C}} = {(\frac{H E}{A B})}^{2} \Rightarrow S_{E H F} = S_{B A C} . {(\frac{H E}{A B})}^{2}$

Vì S_ABC và AB không đổi nên S_EHF nhỏ nhất khi HE nhỏ nhất

Do đó EH ^ AB.

Vậy S_EHF nhỏ nhất khi E là hình chiếu của H trên AB.

Câu 23:

Chứng minh rằng a² + b² + 4 ≥ ab + 2(a + b) với mọi a, b.

Xem đáp án

Hướng dẫn giải

Xét I = a² + b² + 4 - ab - 2(a + b)

Û 2I = 2a² + 2b² + 8 - 2ab - 4(a + b) (nhân 2 vế của phương trình với 2)

Û 2I = 2a² + 2b² + 8 - 2ab - 4a - 4b

Û 2I = (a² - 2ab + 2b²) + (a² - 4a + 4) + (b² - 4b + 4)

Û 2I = (a - b)² + (a - 2)² + (b - 2)² ³ 0 "a, b

Þ I ³ 0 "a, b

Từ đó suy ra a² + b² + 4 - ab - 2(a + b) ³ 0 "a, b

Vậy a² + b² + 4 ≥ ab + 2(a + b) với mọi a, b.