6 câu hỏi trắc nghiệm thuộc Đề kiểm tra cuối kỳ 2 Toán 8 có đáp án ( Mới nhất)_ đề 8

Câu 1:

Cho biểu thức: A = $\frac{x + 3}{x^{2} - 4}$ và B = $\frac{x^{2}}{x^{2} - 4} + \frac{1}{2 - x}$ − $\frac{x}{x + 2}$ (x ≠ ±2)

a) Tính giá trị biểu thức A khi x = 3.

b) Rút gọn B.

c) Cho P = $\frac{B}{A}$ . Tìm x để P < 1.

Xem đáp án

a) Thay x = 3 (thỏa mãn điều kiện) vào biểu thức A = $\frac{x + 3}{x^{2} - 4}$ ta được:

A = $\frac{3 + 3}{3^{2} - 4}$ = $\frac{6}{5}$ .

Vậy với x = 3 thì A = $\frac{6}{5}$ .

b) Với x ≠ ±2 ta có:

Ta có: B = $\frac{x^{2}}{x^{2} - 4} + \frac{1}{2 - x}$ − $\frac{x}{x + 2}$

= $\frac{x^{2}}{(x - 2) (x + 2)} - \frac{1}{x - 2}$ − $\frac{x}{x + 2}$

= $\frac{x^{2}}{(x - 2) (x + 2)}$ − $\frac{(x + 2)}{(x - 2) (x + 2)}$ − $\frac{x (x - 2)}{(x + 2) (x - 2)}$

= $\frac{x^{2} - (x + 2) - x (x - 2)}{(x - 2) (x + 2)}$

= $\frac{x^{2} - x - 2 - x^{2} + 2 x}{(x - 2) (x + 2)}$

= $\frac{x - 2}{(x - 2) (x + 2)}$

= $\frac{1}{x + 2}$ .

Vậy với x ≠ ±2 thì B = $\frac{1}{x + 2} .$

c) Với x ≠ ±2 ta có:

P = $\frac{B}{A}$ = $\frac{1}{x + 2}$ : $\frac{x + 3}{x^{2} - 4}$

= $\frac{1}{x + 2}$ . $\frac{x^{2} - 4}{x + 3}$

= $\frac{1}{x + 2}$ . $\frac{(x - 2) (x + 2)}{x + 3}$

= $\frac{x - 2}{x + 3}$

Ta có:

P < 1 $\Leftrightarrow$ $\frac{x - 2}{x + 3}$ < 1

$\Leftrightarrow$ $\frac{x - 2}{x + 3}$ − 1 < 0

$\Leftrightarrow$ $\frac{x - 2 - x - 3}{x + 3}$ < 0

$\Leftrightarrow$ $\frac{- 5}{x + 3}$ < 0

Û x + 3 > 0 (vì –5 < 0)

$\Leftrightarrow$ x > −3

Kết hợp điều kiện x ≠ ±2 ta có:

x > −3 và x ≠ ±2.

Vậy với x > −3 và x ≠ ±2 thì P < 1.

Câu 2:

Giải bài toán bằng cách lập phương trình

Hai ô tô khởi hành một lúc tại A để đi đến B. Ô tô thứ nhất đi với vận tốc 40 km/h. Ô tô thứ hai đi với vận tốc 50 km/h. Biết rằng ô tô thứ nhất tới B chậm hơn ô tô thứ hai 30 phút. Tính độ dài quãng đường AB.

Xem đáp án

Gọi s (km) là quãng đường AB (s > 0)

Thời gian mà ô tô thứ nhất đi từ A đến B là: $\frac{s}{40}$ (giờ)

Thời gian mà ô tô thứ hai đi từ A đến B là: $\frac{s}{50}$ (giờ)

Theo đề bài ô tô thứ nhất tới chậm hơn ô tô thứ hai 30 phút (0,5 giờ) vậy nên ta có:

$\frac{s}{40}$ − $\frac{s}{50}$ = 0,5

$\Leftrightarrow \frac{50 s - 40 s}{2000} = 0, 5$

Û 50s – 40s = 1 000

Û 10s = 1 000

Û s = 100 (km)

Vậy quãng đường AB dài 100 km.

Câu 3:

Giải bất phương trình sau và biểu diễn tập nghiệm trên trục số:

$\frac{x - 3}{3}$ − $\frac{2 x - 1}{2}$ > 2

Xem đáp án

Ta có: $\frac{x - 3}{3}$ − $\frac{2 x - 1}{2}$ > 2

Û $\frac{6. (x - 3)}{3}$ − $\frac{6. (2 x - 1)}{2}$ > 6.2

Û $\frac{3.2. (x - 3)}{3}$ − $\frac{2.3. (2 x - 1)}{2}$ > 12

Û 2.(x – 3) – 3.(2x – 1) > 12

Û 2x − 6 − 6x + 3 > 12

Û 2x − 6x > 12 + 6 − 3

Û −4x > 15

Û x < −3,75

Vậy tập nghiệm của bất phương trình là: S = {x| x < −3,75}.

Biểu diễn tập nghiệm trên trục số:

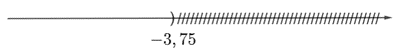
Câu 4:

Cho biết một bể bơi tiêu chuẩn có chiều dài 50 m, chiều rộng 25 m và chiều cao 2,3 m. Người ta bơm nước vào bể sao cho nước cách mép bể 0,5 m. Tính số lít nước đã bơm vào bể.

Xem đáp án

Chiều cao của mực nước là:

2,3 – 0,5 = 1,8 (m)

Số lít nước đã bơm vào bể là:

50.25.1,8 = 2 250 (m³) = 2 250 000 (lít)

Vậy người ta đã bơm vào bể 2 250 000 lít nước.

Câu 5:

Cho ∆ ABC nhọn, đường cao AH. Kẻ HE ⊥ AB (E ∈ AB), HF ⊥ AC (F ∈ AC).

a) Chứng minh: ∆AEH ∽ ∆AHB. Từ đó suy ra AH² = AE.AB.

b) Chứng minh AE. AB = AF.AC.

c) Cho chu vi các ∆AEF và ∆ACB lần lượt là 20 cm và 30 cm. Tính diện tích ∆AEF và ∆ACB biết diện tích ∆ACB lớn hơn diện tích ∆AEF là 25 cm².

Xem đáp án

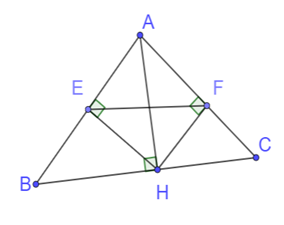
a) Vì AH là đường cao (giả thiết)

Þ AH ⊥ BC

Þ ∆AHB vuông tại H

Lại có HE ⊥ AB (giả thiết)

Þ ∆AEH vuông tại E

Do đó $\hat{A E H}$ = $\hat{A H B}$ = 90°

Xét ∆AEH và ∆AHB có:

$\hat{A E H}$ = $\hat{A H B}$ (chứng minh trên),

$\hat{B A H}$ chung

Do đó ∆AEH ∽ ∆ AHB (g.g)

Þ $\frac{A H}{A B}$ = $\frac{A E}{A H}$ (tỉ số đồng dạng)

Þ AH² = AE.AB. (1)

b) Vì AH ⊥ BC (chứng minh câu a)

Þ $\hat{A H C}$ = 90°

Vì HF ⊥ AC (giả thiết)

Þ $\hat{A F H}$ = 90°

Xét ∆AFH và ∆AHC có

$\hat{A F H}$ = $\hat{A H C}$ = 90°,

$\hat{H A F}$ chung

Do đó ∆AFH ᔕ ∆AHC (g.g)

Þ $\frac{A F}{A H}$ = $\frac{A H}{A C}$ (tỉ số đồng dạng)

Þ AH² = AF. AC (2)

Từ (1) và (2) suy ra: AE. AB = AF.AC.

c) Theo câu b có: AE. AB = AF.AC

Þ $\frac{A E}{A C}$ = $\frac{A F}{A B}$

Xét ∆AEF và ∆ACB có

$\hat{A}$ chung,

$\frac{A E}{A C}$ = $\frac{A F}{A B}$ (chứng minh trên)

Do đó ∆AEF ᔕ ∆ACB (c.g.c)

Þ $\frac{A E}{A C}$ = $\frac{A F}{A B}$ = $\frac{E F}{B C}$ (tỉ số đồng dạng)

Theo tính chất dãy tỉ số bằng nhau ta có:

$\frac{A E}{A C}$ = $\frac{A F}{A B}$ = $\frac{E F}{B C}$ = $\frac{A E + A F + E F}{A C + A B + B C} = \frac{20}{30} = \frac{2}{3}$

(vì chu vi ∆AEF và ∆ACB lần lượt là 20 cm và 30 cm)

Þ $\frac{S_{A E F}}{S_{A B C}}$ = ${(\frac{A E}{A C})}^{2}$ = ${(\frac{2}{3})}^{2}$ = $\frac{4}{9}$

$\Rightarrow \frac{S_{A E F}}{4} = \frac{S_{A B C}}{9}$ (tính chất tỉ lệ thức)

Áp dụng tính chất dãy tỉ số bằng nhau ta có:

\frac{S_{A E F}}{4} = \frac{S_{A B C}}{9} = \frac{S_{A B C} - S_{A E F}}{9 - 4} = \frac{25}{5} = 5

(do S_ABC – S_AEF = 25 (cm²))

Þ S_AEF = 5.4 = 20 (cm²)

Và S_ABC = 5.9 = 45 (cm²)

Vậy S_AEF = 20 cm² và S_ABC = 45 cm².

Câu 6:

Cho x > 1; y > 1 và x + y = 6. Tìm giá trị nhỏ nhất của:

S = 3x + 4y $+ \frac{5}{x - 1} + \frac{9}{y - 1}$

Xem đáp án

Với x > 1; y > 1 và x + y = 6 ta có:

S = 3x + 4y + $\frac{5}{x - 1}$ + $\frac{9}{y - 1}$

= $(\frac{5}{4} x + \frac{7}{4} x)$ + $(\frac{9}{4} y + \frac{7}{4} y)$ + $\frac{5}{x - 1}$ + $\frac{9}{y - 1}$ – $\frac{5}{4}$ – $\frac{9}{4}$ + $\frac{7}{2}$

= $\frac{5}{4}$ x – $\frac{5}{4}$ + $\frac{5}{x - 1}$ + $\frac{9}{4}$ y – $\frac{9}{4}$ + $\frac{9}{y - 1}$ + $\frac{7}{4}$ x + $\frac{7}{4}$ y + $\frac{7}{2}$

= $\frac{5}{4}$ . (x – 1) + $\frac{5}{x - 1}$ + $\frac{9}{4}$ . (y – 1) + $\frac{9}{y - 1}$ + $\frac{7}{4}$ . (x + y) + $\frac{7}{2}$

= $\frac{7}{2}$ . (x – 1) + $\frac{5}{x - 1}$ + $\frac{9}{4}$ . (y – 1) + $\frac{9}{y - 1}$ + $\frac{7}{4}$ . 6 + $\frac{7}{2}$

= $\frac{5}{4}$ . (x – 1) + $\frac{5}{x - 1}$ + $\frac{9}{4}$ . (y – 1) + $\frac{9}{y - 1}$ + 14

Với x > 1; y > 1, áp dụng bất đẳng thức Cosi cho hai số không âm $\frac{5}{4}$ . (x – 1) và $\frac{5}{x - 1}$ ta có:

$\frac{5}{4}$ . (x – 1) + $\frac{5}{x - 1}$ ≥ 2 $\sqrt{\frac{5}{4} (x - 1) . \frac{5}{(x - 1)}}$

Þ $\frac{5}{4}$ . (x – 1) + $\frac{5}{x - 1}$ ≥ 2. $\sqrt{\frac{25}{4}}$ = 2. $\frac{5}{2}$ = 5

Với x > 1; y > 1, áp dụng bất đẳng thức Cosi cho hai số không âm $\frac{9}{4}$ . (y – 1) và $\frac{9}{y - 1}$ ta có:

$\frac{9}{4}$ . (y – 1) + $\frac{9}{y - 1}$ ≥ 2 $\sqrt{\frac{9}{4} (y - 1) . \frac{9}{(y - 1)}}$

Þ $\frac{9}{4}$ . (y – 1) + $\frac{9}{y - 1}$ ≥ 2 $\sqrt{\frac{81}{4}}$ = 2 . $\frac{9}{2}$ = 9

Do đó:

S ≥ 5 + 9 + 14 = 28

Dấu “=” xảy ra khi và chỉ khi:

$\{\begin{cases} \frac{5}{4} (x - 1) = \frac{5}{x - 1} \\ \frac{9}{4} (y - 1) = \frac{9}{y - 1} \\ x + y = 6 \end{cases}$

$\Leftrightarrow \{\begin{cases} x - 1 = 2 \\ y - 1 = 2 \\ x + y = 6 \end{cases}$ (do x > 1; y > 1)

$\Leftrightarrow \{\begin{cases} x = 3 \\ y = 3 \\ x + y = 6 \end{cases}$

Vậy S_min= 28 với x = y = 3.