5 câu hỏi trắc nghiệm thuộc Đề kiểm tra cuối kỳ 2 Toán 8 có đáp án ( Mới nhất)_ đề 6

Câu 1:

Giải các phương trình và bất phương trình sau:

a) |x + 5| = 3x + 1;

b) $\frac{x + 6}{5} - \frac{x - 2}{3} < 2$ ;

c) $\frac{x - 2}{x + 2} - \frac{3}{x - 2} = \frac{2 (x - 11)}{x^{2} - 4}$

Xem đáp án

a) |x + 5| = 3x + 1

• Với x ≥ − 5 thì |x + 5| = x + 5.

Khi đó: x + 5 = 3x + 1

Û 3x – x = 5 – 1

Û 2x = 4

Û x = 2 (TM).

• Với x < − 5 thì |x + 5| = – x – 5.

Khi đó: – x – 5 = 3x + 1

Û 3x + x = – 5 – 1

Û 4x = – 6

$\Leftrightarrow x = \frac{- 3}{2}$ (loại).

Vậy tập nghiệm của phương trình đã cho là S = {2}.

b) $\frac{x + 6}{5} - \frac{x - 2}{3} < 2$

$\Leftrightarrow \frac{3 (x + 6)}{15} - \frac{5 (x - 2)}{15} < \frac{30}{15}$

Û 3(x + 6) – 5(x – 2) < 30

Û 3x + 18 – 5x + 10 < 30

Û – 2x + 28 < 30

Û – 2x < 2

Û x > –1.

Vậy tập nghiệm của bất phương trình đã cho là S = {x | x > –1}.

c) $\frac{x - 2}{x + 2} - \frac{3}{x - 2} = \frac{2 (x - 11)}{x^{2} - 4}$

ĐKXĐ: ${\begin{cases} x + 2 \neq 0 \\ x - 2 \neq 0 \end{cases} \Leftrightarrow x \neq \pm 2$ .

Phương trình đã cho tương đương:

$\frac{x - 2}{x + 2} - \frac{3}{x - 2} = \frac{2 (x - 11)}{(x + 2) (x - 2)}$

$\Leftrightarrow \frac{{(x - 2)}^{2}}{(x + 2) (x - 2)} - \frac{3 (x + 2)}{(x + 2) (x - 2)} = \frac{2 (x - 11)}{(x + 2) (x - 2)}$

Þ (x – 2)² – 3(x + 2) = 2(x – 11)

Û x² – 4x + 4 – 3x – 6 = 2x – 22

Û x² – 7x – 2 = 2x – 22

Û x² – 9x + 20 = 0

Û (x² – 4x) – (5x – 20) = 0

Û x(x – 4) – 5(x – 4) = 0

Û (x – 4)(x – 5) = 0

Û x – 4 = 0 hoặc x – 5 = 0

Û x = 4 (TM) hoặc x = 5 (TM).

Vậy tập nghiệm của phương trình đã cho là S = {4; 5}.

Câu 2:

Một bạn học sinh đi học từ nhà đến trường với vận tốc trung bình 4 km/h. Sau khi đi được $\frac{2}{3}$ quãng đường, bạn ấy đã tăng vận tốc lên 5 km/h. Tính quãng đường từ nhà đến trường của bạn học sinh đó, biết rằng thời gian bạn ấy đi từ nhà đến trường là 28 phút.

Xem đáp án

Gọi x (km) là quãng đường từ nhà đến trường của bạn học sinh (x > 0).

Quãng đường đi với vận tốc 4 km/h là $\frac{2}{3} x$ (km).

Thời gian đi $\frac{2}{3}$ quãng đường đó là: $\frac{2}{3} x : 4 = \frac{x}{6}$ (giờ).

Quãng đường đi với vận tốc 5 km/h là $\frac{1}{3} x$ (km).

Thời gian đi $\frac{1}{3}$ quãng đường còn lại là: $\frac{1}{3} x : 5 = \frac{x}{15}$ (giờ).

Đổi 28 phút = $\frac{7}{15}$ giờ.

Thời gian đi hết quãng đường là 28 phút hay $\frac{7}{15}$ giờ nên ta có phương trình:

$\frac{x}{6} + \frac{x}{15} = \frac{7}{15}$

$\Leftrightarrow \frac{x}{2} + \frac{x}{5} = \frac{7}{5}$

$\Leftrightarrow \frac{5 x}{10} + \frac{2 x}{10} = \frac{14}{10}$

Û 5x + 2x = 14

Û 7x = 14

Û x = 2 (TMĐK).

Vậy quãng đường từ nhà đến trường của bạn học sinh đó là 2 km.

Câu 3:

Cho tam giác ABC vuông tại A có AB = 6 cm, AC = 8 cm. Kẻ đường cao AH.

a) Chứng minh: DABC đồng dạng với DHBA.

b) Chứng minh: AH² = HB . HC.

c) Tính độ dài các cạnh BC, AH.

d) Phân giác của góc ACB cắt AH tại E, cắt AB tại D. Tính tỉ số diện tích của hai tam giác ACD và HCE.

Xem đáp án

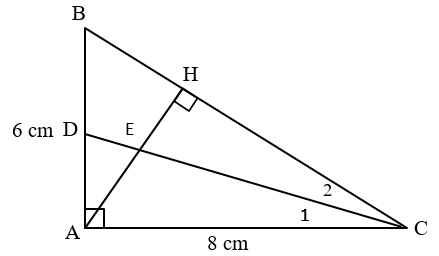
a) Xét DABC và DHBA có:

$\hat{B A C} = \hat{A H B} = 90^{o}$

chung

Do đó DABC DHBA (g.g).

b) Chứng minh: AH² = HB . HC.

Xét DABH và DCAH có:

$\hat{A H B} = \hat{A H C} = 90^{o}$ (vì $A H ⊥ B C$ ).

$\hat{B A H} = \hat{A C H}$ (cùng phụ $\hat{C A H}$ ).

Do đó DABH DCAH (g.g).

c) Áp dụng định lý Py-ta-go vào DABC vuông tại A, ta có:

$B C = \sqrt{A B^{2} + A C^{2}} = \sqrt{6^{2} + 8^{2}} = 10$ (cm).

Từ câu a: DABC DHBA nên: $\frac{A C}{H A} = \frac{B C}{B A}$ .

Suy ra: $H B = \frac{A B^{2}}{B C} = \frac{6^{2}}{10} = 3,6$ (cm).

Vậy BC = 10 cm; AH = 4,8 cm.

d) Từ câu a: DABC DHBA nên: $\frac{A B}{H B} = \frac{B C}{B A}$ .

Suy ra: $\hat{C A D} = \hat{A H C} = 90^{o}$ (cm).

Do đó: HC = BC – HB = 10 – 3,6 = 6,4 (cm).

Xét DACD và DHCE có:

$\hat{C A D} = \hat{A H C} = 90^{o}$

${\hat{C}}_{1} = {\hat{C}}_{2}$ (vì CD là tia phân giác của $\hat{A C B}$ )

Do đó DACD

Suy ra $\frac{S_{A C D}}{S_{H C E}} = {(\frac{A C}{H C})}^{2} = {(\frac{8}{6,4})}^{2} = \frac{25}{16}$ .

Câu 4:

Tính diện tích toàn phần và thể tích của hình lăng trụ đứng có đáy là tam giác vuông theo các kích thước ở hình sau:

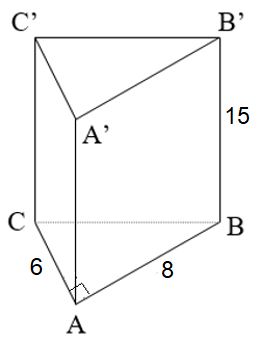
Tính diện tích toàn phần và thể tích của hình lăng trụ đứng có đáy là tam giác vuông theo các kích thước ở hình sau: (ảnh 1)

Xem đáp án

Xét ∆ABC vuông tại A, áp dụng định lý Py-ta-go, ta có:

BC² = AB² + AC² = 6² + 8² = 100.

Suy ra: BC = 10 cm.

Diện tích xung quanh của hình lăng trụ đứng là:

S_xq = (6 + 8 + 10) . 15 = 360 (cm²).

Diện tích đáy của hình lăng trụ đứng là:

$S_{đ} = \frac{1}{2} . 6 . 8 = 24$ (cm²).

Diện tích toàn phần của hình lăng trụ là:

S_tp = S_xq + S_2đ = 360 + 2 . 24 = 408 (cm²).

Thể tích của hình lăng trụ đứng là:

V = S_đ . h = 24 . 15 = 360 (cm³).

Vậy hình lăng trụ đứng có diện tích toàn phần là 360 cm² và thể tích là 360 cm³.

Câu 5:

Cho ba số x, y, z dương và đôi một khác nhau thỏa mãn

\frac{1}{x} + \frac{1}{y} + \frac{1}{z} = 0.

Tính giá trị của biểu thức:

A = \frac{y z}{x^{2} + 2 y z} + \frac{x z}{y^{2} + 2 x z} + \frac{x y}{z^{2} + 2 x y}

.

Xem đáp án

Ta có: $\frac{1}{x} + \frac{1}{y} + \frac{1}{z} = 0 \Leftrightarrow \frac{x y + y z + x z}{x y z} = 0$ .

Mà ba số x, y, z dương nên: xyz > 0.

Nên: xy + yz + xz = 0

Û yz = – xy – xz.

Ta có: x²+ 2yz = x²+ yz – xy – xz

= x(x – y) – z(x – y) = (x – y)(x – z).

Tương tự: y²+ 2xz = (y – x)(y – z);

z²+ 2xy = (z – x)(z – y).

Do đó: $A = \frac{y z}{x^{2} + 2 y z} + \frac{x z}{y^{2} + 2 x z} + \frac{x y}{z^{2} + 2 x y}$

$= \frac{y z}{(x - y) (x - z)} + \frac{x z}{(y - x) (y - z)} + \frac{x y}{(z - x) (z - y)}$

$= \frac{- y z (y - z)}{(x - y) (y - z) (z - x)} - \frac{x z (z - x)}{(x - y) (y - z) (z - x)} - \frac{x y (x - y)}{(x - y) (y - z) (z - x)}$

$= \frac{- y z (y - z) - x z (z - x) - x y (x - y)}{(x - y) (y - z) (z - x)}$

$= \frac{- y z (y - z) + x z (y - z) + x z (x - y) - x y (x - y)}{(x - y) (y - z) (z - x)}$

$= \frac{(y - z) (x z - y z) + (x - y) (x z - x y)}{(x - y) (y - z) (z - x)}$

$= \frac{z (x - y) (y - z) - x (x - y) (y - z)}{(x - y) (y - z) (z - x)}$

$= \frac{(x - y) (y - z) (z - x)}{(x - y) (y - z) (z - x)} = 1$ .

Vậy $A = \frac{y z}{x^{2} + 2 y z} + \frac{x z}{y^{2} + 2 x z} + \frac{x y}{z^{2} + 2 x y} = 1$ .