20 câu hỏi trắc nghiệm thuộc Đề kiểm tra cuối kỳ 2 Toán 8 có đáp án ( Mới nhất)_ đề 21

Câu 1:

Phương trình 3x + 1 = -x + 9 có nghiệm là

A. x = 2;

B. x = 5;

C. x = -2;

D. x = 3.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: A

3x + 1 = -x + 9

Û 3x + x = 9 - 1

Û 4x = 8 Û x = 2

Vậy tập nghiệm của phương trình là S = {2}.

Câu 2:

Nghiệm của bất phương trình 4 - 2x < 6 là

A. x > -5;

B. x < -5;

C. x < -1;

D. x > -1.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: D

4 - 2x < 6

Û 2x > 4 - 6

Û 2x > -2 Û x > -1

Vậy tập nghiệm của bất phương trình là S = {x | x > -1}

Câu 3:

Hai biểu thức $\frac{4 x^{2}}{3 - 2 x}$ và $\frac{9}{3 - 2 x}$ có giá trị bằng nhau khi và chỉ khi

A. $x = - \frac{3}{2};$

B. $x = \pm \frac{3}{2};$

C. $x = \frac{3}{2};$

D. $x = - \frac{9}{4} .$

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: A

ĐKXĐ:

3 - 2x ¹ 0 $\Leftrightarrow x \neq \frac{3}{2}$

Hai biểu thức $\frac{4 x^{2}}{3 - 2 x}$ và $\frac{9}{3 - 2 x}$ có giá trị bằng nhau khi và chỉ khi

$\frac{4 x^{2}}{3 - 2 x} = \frac{9}{3 - 2 x}$

Þ 4x² = 9 $\Leftrightarrow x^{2} = \frac{9}{4}$

$x = \pm \sqrt{\frac{9}{4}} = \pm \frac{3}{2}$

Áp dụng ĐKXĐ ta thấy $x = - \frac{3}{2}$ thỏa mãn

Vậy để hai biểu thức có giá trị bằng nhau khi và chỉ khi $x = - \frac{3}{2}$ .

Câu 4:

Trong các bất phương trình sau, bất phương trình nào là bất phương trình bậc nhất một ẩn?

A. 2x + y > 0;

B. 2x² - 6 < 0;

C. 2x + 5 ³ 0;

D. x(x + 1) > 0.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: C

+) 2x + y > 0

Đây không là phương trình bậc nhất một ẩn vì xuất hiện hai ẩn x và y

+) 2x² - 6 < 0

Đây là phương trình bậc hai một ẩn

+) 2x + 5 ³ 0

Đây là phương tình bậc nhất một ẩn

+) x(x + 1) > 0

Û x² + x > 0

Đây là phương trình bậc hai một ẩn.

Câu 5:

Số nghiệm của phương trình (1 - x)² + 2x = x² + 1 là

A. Một nghiệm;

B. Hai nghiệm;

C. Vô nghiệm;

D. Vô số nghiệm.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: D

(1 - x)² + 2x = x² + 1

Û 1 - 2x + x² + 2x = x² + 1

Û 1 + x² = x² + 1 (Luôn đúng với mọi x)

Vậy đây là phương trình có vô số nghiệm

Câu 6:

Tất cả các giá trị của k để phương trình 4x² - 25 + k² + 4kx = 0 có nghiệm x = -2 là

A. k = -1;

B. k = 9;

C. k = -1; k = 9;

D. k = 1; k = -9.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: C

Để phương trình 4x² - 25 + k² + 4kx = 0 có nghiệm x = -2 thì

4.(-2)² - 25 + k² + 4k.(-2) = 0

Û 16 - 25 + k² - 8k = 0

Û k² - 8k - 9 = 0

Û k² - 9k + k - 9 = 0

Û k(k - 9) + (k - 9) = 0

Û (k - 9)(k + 1) = 0

$\Rightarrow [\begin{matrix} k - 9 = 0 \\ k + 1 = 0 \end{matrix} \Leftrightarrow [\begin{matrix} k = 9 \\ k = - 1 \end{matrix}$

Vậy các giá trị k thỏa mãn là k = -1; k = 9.

Câu 7:

Cho đoạn thẳng AB = 2 dm và CD = 3 m, tỉ số của hai đoạn thẳng này là

A. $\frac{A B}{C D} = \frac{2}{3};$

B. $\frac{A B}{C D} = \frac{3}{2};$

C. $\frac{A B}{C D} = \frac{1}{15};$

D. $\frac{A B}{C D} = \frac{15}{1} .$

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: C

Đổi CD = 3 m = 30 dm

Tỉ số của hai đoạn thẳng này là

$\frac{A B}{C D} = \frac{2}{30} = \frac{1}{15} .$

Câu 8:

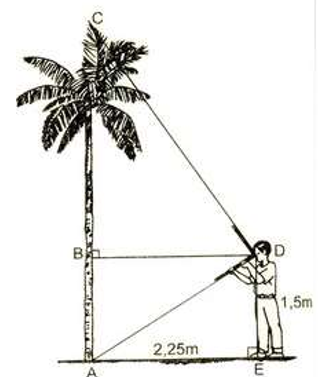
Một người thợ sử dụng thước ngắm có góc vuông để đo gián tiếp chiều cao của một cái cây. Với các kích thước đo được như hình bên: Khoảng cách từ vị trí gốc cây đến vị trí chân của người thợ là 2,25 m và từ vị trí chân đứng thẳng trên mặt đất đến mắt của người ngắm là 1,5 m. Hỏi với các kích thước trên thì người thợ đo được chiều cao của cây đó là bao nhiêu?

Một người thợ sử dụng thước ngắm có góc vuông để đo gián tiếp chiều cao của một cái cây. Với các kích thước đo được như hình bên: (ảnh 1)

A. 3,25 m;

B. 4,875 m;

C. 5,625 m;

D. 4,5 m.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: B

Ta có:

+) AEDB là hình chữ nhật nên suy ra AB = DE = 1,5 m và BD = AE = 2,25 m

+) Áp dụng định lý Pytago vào tam giác AED vuông tại E có

$A D = \sqrt{A E^{2} + D E^{2}} = \sqrt{{2,25}^{2} + {1,5}^{2}} = \frac{3 \sqrt{13}}{4} m$

+) Xét hai tam giác ABD và ADC có:

$\begin{matrix} \hat{B A D} = \hat{D A C} (\hat{A} c h u n g) \\ \hat{A B D} = \hat{A D C} (= 90 °) \end{matrix}\} \Rightarrow Δ A B D ∽ Δ A D C (g . g)$

$\Rightarrow \frac{A B}{A D} = \frac{A D}{A C}$

$\Leftrightarrow A C = \frac{A D^{2}}{A B} = \frac{{(\frac{3 \sqrt{13}}{4})}^{2}}{1,5} = 4,875 m$

Vậy chiều cao của của cây đó là 4,875 m.

Câu 9:

Cho ∆ABC vuông tại A có AB = 3cm, BC = 5cm, AD là đường phân giác trong của góc A (D thuộc BC). Tỉ số $\frac{D B}{D C}$ bằng

A. $\frac{3}{5};$

B. $\frac{5}{3};$

C. $\frac{4}{3};$

D. $\frac{3}{4} .$

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: D

Áp dụng định lý Py-ta-go vào tam giác ABC vuông tại A có:

$A C = \sqrt{B C^{2} - A B^{2}} = \sqrt{5^{2} + 3^{2}} = 4 (m)$

Ta thấy ∆ABC vuông tại A có AD là đường phân giác trong của góc A (D Î BC).

Áp dụng tính chất đường phân giác vào tam giác ABC có:

$\frac{D B}{D C} = \frac{A B}{A C} = \frac{3}{4} .$

Câu 10:

Hình hộp chữ nhật có:

A. 6 đỉnh, 8 mặt, 12 cạnh;

B. 8 đỉnh, 6 mặt, 12 cạnh;

C. 12 đỉnh, 6 mặt, 8 cạnh;

D. 6 đỉnh, 12 mặt, 8 cạnh.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: B

Hình hộp chữ nhật có: 8 đỉnh, 6 mặt, 12 cạnh.

Câu 11:

Nếu ∆ABC có MN // BC, (M Î AB, N Î AC) theo định lý Talet ta có:

A. $\frac{A M}{M B} = \frac{A N}{N C};$

B. $\frac{A M}{A B} = \frac{A N}{N C};$

C. $\frac{A M}{M B} = \frac{A N}{A C};$

D. $\frac{A B}{M B} = \frac{A N}{N C} .$

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: A

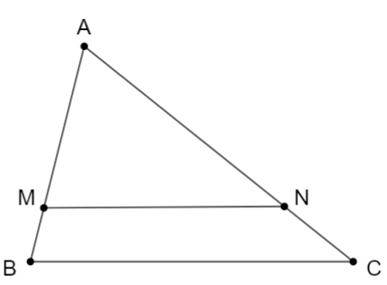
Nếu ∆ABC có MN // BC, (M thuộc AB, N thuộc AC) theo định lý Talet ta có: (ảnh 1)

Nếu ∆ABC có MN // BC, (M Î AB, N Î AC) theo định lý Ta-let, ta có:

$\frac{A M}{M B} = \frac{A N}{N C} .$

Câu 12:

Cho tam giác ABC có AB = 9cm; AC = 12cm; BC = 15cm. Trên cạnh AB và AC lần lượt lấy hai điểm M và N sao cho AM = 3cm, AN = 4cm. Kết luận nào sau đây là sai?

A. MN // BC;

B. $\frac{A N}{B C} = \frac{M N}{A C};$

C. $\frac{A M}{A B} = \frac{A N}{A C};$

D. DANM vuông.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: B

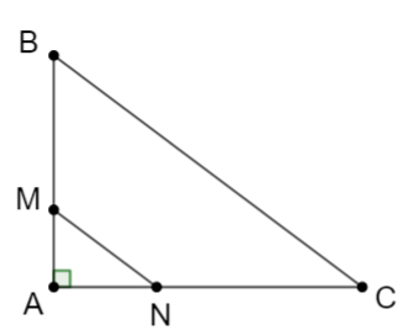
Cho tam giác ABC có AB = 9cm; AC = 12cm; BC = 15cm. Trên cạnh AB và AC lần lượt lấy hai điểm (ảnh 1)

+) Xét tam giác ABC có:

BC² = AB² + AC² (15² = 9² + 12²)

Theo định lý Py-ta-go đảo nên suy ra tam giác ABC vuông tại A, ta có:

$\frac{A M}{A B} = \frac{A N}{A C} (\frac{3}{9} = \frac{4}{12} = \frac{1}{3})$

Theo định lý Ta-lét đảo nên suy ra MN // BC, ta có:

$\frac{A N}{A C} = \frac{M N}{B C} \Leftrightarrow A N . B C = M N . A C$

Tam giác ABC vuông tại A nên tam giác AMN vuông tại A.

Câu 13:

Giải các phương trình và bất phương trình sau:

a) 3x + 1 = 7x - 11;

Xem đáp án

Hướng dẫn giải

a) 3x + 1 = 7x - 11

Û 7x - 3x = 1 + 11

Û 4x = 12

Û x = 3

Vậy tập nghiệm của phương trình là S = {3}.

Câu 14:

Giải các phương trình và bất phương trình sau:

b) $\frac{x - 1}{x + 2} - \frac{x}{x - 2} = \frac{4 - 6 x}{x^{2} - 4};$

Xem đáp án

b) ĐKXĐ: $\{\begin{matrix} x - 2 \neq 0 \\ x + 2 \neq 0 \end{matrix} \Leftrightarrow \{\begin{matrix} x \neq 2 \\ x \neq - 2 \end{matrix}$

$\frac{x - 1}{x + 2} - \frac{x}{x - 2} = \frac{4 - 6 x}{x^{2} - 4}$

$\Leftrightarrow \frac{x - 1}{x + 2} - \frac{x}{x - 2} = \frac{4 - 6 x}{(x - 2) (x + 2)}$

$\Leftrightarrow \frac{(x - 1) (x - 2)}{(x - 2) (x + 2)} - \frac{x (x + 2)}{(x - 2) (x + 2)} = \frac{4 - 6 x}{(x - 2) (x + 2)}$

$\Leftrightarrow \frac{x^{2} - x - 2 x + 2}{(x - 2) (x + 2)} - \frac{x^{2} + 2 x}{(x - 2) (x + 2)} = \frac{4 - 6 x}{(x - 2) (x + 2)}$

$\Leftrightarrow \frac{- 5 x + 2}{(x - 2) (x + 2)} = \frac{4 - 6 x}{(x - 2) (x + 2)}$

Þ -5x + 2 = 4 - 6x

Û 6x - 5x = 4 - 2

Û x = 2 (không thỏa mãn ĐKXĐ)

Vậy phương trình đã cho vô nghiệm.

Câu 15:

Giải các phương trình và bất phương trình sau:

c) $1 + \frac{x + 4}{5} \leq x - \frac{x + 3}{3} .$

Xem đáp án

c)

$1 + \frac{x + 4}{5} \leq x - \frac{x + 3}{3}$

$\Leftrightarrow \frac{5 + x + 4}{5} \leq \frac{3 x - x - 3}{3}$

$\Leftrightarrow \frac{x + 9}{5} \leq \frac{2 x - 3}{3}$

Û 3(x + 9) £ 5(2x - 3)

Û 3x + 27 £ 10x - 15

Û 10x - 3x ³ 27 + 15

Û 7x ³ 42

Û x ³ 6

Vậy tập nghiệm của bất phương trình là S = {x | x ³ 6}.

Câu 16:

Trong chuyến tham quan thực tế tại một trang trại chăn nuôi, bạn An hỏi một anh công nhân số con gà và số con bò trang trại đang nuôi thì được anh công nhân cười và nói rằng: “Tất cả có 1200 con và 2700 chân”. Bạn tính giúp bạn An xem có bao nhiêu con gà, bao nhiêu con bò nhé!

Xem đáp án

Hướng dẫn giải

Gọi x (con) là số gà (x Î ℕ*)

Khi đó số chân gà là 2x (chân)

Tổng số con gà và bò là 1 200 con nên số con bò là 1200 − x (con)

Số chân bò là 4(1 200 – x) (chân)

Vì tổng số chân gà và chân bò là 2 700 chân nên ta có phương trình

2x + 4(1200 − x) = 2700

Û 2x + 4800 ‒ 4x = 2700

Û ‒2x = 2700 ‒ 4800

Û ‒2x = −2100

Û x = 1 050 (thỏa mãn)

Vậy số gà là 1 050 con và số bò là 1 200 ‒ 1050 = 150 (con).

Câu 17:

Cho ∆ABC vuông tại A, đường cao AH.

a) Chứng minh ∆ABC đồng dạng với ∆HBA, từ đó suy ra AB² = BH.BC.

Xem đáp án

Hướng dẫn giải

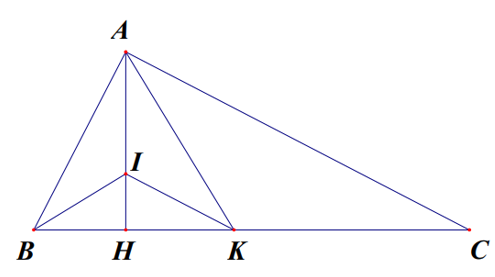
Cho ∆ABC vuông tại A, đường cao AH. a) Chứng minh ∆ABC đồng dạng với ∆HBA, từ đó suy ra AB2 = BH.BC. (ảnh 1)

a) Xét hai tam giác DABH và DCBA có

$\begin{matrix} \hat{A B H} = \hat{C B A} (\hat{B} c h u n g) \\ \hat{A H B} = \hat{C A B} (= 90 °) \end{matrix}\} \Rightarrow Δ A B H ∽ Δ C B A (g . g)$

$\Rightarrow \frac{A B}{C B} = \frac{B H}{B A} \Leftrightarrow A B^{2} = B H . B C$ (đpcm)

Câu 18:

b) Tia phân giác của góc ABC cắt AH tại I. Chứng minh rằng: $\frac{I A}{I H} = \frac{A C}{H A} .$

Xem đáp án

b) Ta có:

+) ∆ABC ᔕ ∆HBA (cmt)

$\Rightarrow \frac{A B}{H B} = \frac{A C}{H A}$ (1)

Áp dụng tính chất đường phân giác vào tam giác ABH có BI là đường phân giác

$\Rightarrow \frac{A B}{H B} = \frac{A I}{H I}$ (2)

Từ (1) và (2) nên suy ra $\Rightarrow \frac{A C}{H A} = \frac{A I}{H I}$ (đpcm) (3)

Câu 19:

c) Tia phân giác của góc HAC cắt BC tại K. Chứng minh IK song song với AC.

Xem đáp án

c) Áp dụng tính chất đường phân giác vào tam giác ACH có AK là đường phân giác

$\Rightarrow \frac{A C}{H A} = \frac{C K}{H K}$ (4)

Từ (3) và (4) suy ra $\Rightarrow \frac{A I}{H I} = \frac{C K}{H K}$

Tam giác HAC có $\frac{A I}{H I} = \frac{C K}{H K}$ , áp dụng định lý Ta-lét đảo ta suy ra được:

IK // AC (đpcm).

Câu 20:

Cho $f (x) = \frac{x^{2}}{x^{2} + {(x - 1)}^{2}}$ . Hãy tính giá trị của biểu thức sau:

$A = f (\frac{1}{2021}) + f (\frac{2}{2021}) + ... + f (\frac{2019}{2021}) + f (\frac{2020}{2021}) .$

Xem đáp án

Hướng dẫn giải

Ta có: $f (x) = \frac{x^{2}}{x^{2} + {(x - 1)}^{2}}$

$\Rightarrow f (1 - x) = \frac{{(1 - x)}^{2}}{{(1 - x)}^{2} + {(1 - x - 1)}^{2}} = \frac{{(1 - x)}^{2}}{{(1 - x)}^{2} + x^{2}}$

Khi đó: $f (x) + f (1 - x) = \frac{x^{2}}{x^{2} + {(x - 1)}^{2}} + \frac{{(1 - x)}^{2}}{{(1 - x)}^{2} + x^{2}}$

$= \frac{x^{2} + {(1 - x)}^{2}}{x^{2} + {(x - 1)}^{2}} = 1$

Ta xét hai dãy:

$A = f (\frac{1}{2021}) + f (\frac{2}{2021}) + ... + f (\frac{2019}{2021}) + f (\frac{2020}{2021})$

$A = f (\frac{2020}{2021}) + f (\frac{2019}{2021}) + ... + f (\frac{2}{2021}) + f (\frac{1}{2021})$

+) (1)

+) (2)

Cộng vế với vế của (1) và (2) ta có:

$2 A = [f (\frac{1}{2021}) + f (\frac{2020}{2021})] + [f (\frac{2}{2021}) + f (\frac{2019}{2021})] + ... + [f (\frac{2020}{2021}) + f (\frac{1}{2021})]$

Û 2A = 1 + 1 + ... + 1

Û 2A = 2020 Û A = 1010

Vậy A = 1010.