22 câu hỏi trắc nghiệm thuộc Đề kiểm tra cuối kỳ 2 Toán 8 có đáp án ( Mới nhất)_ đề 20

Câu 1:

Trong các phương trình sau, phương trình nào là phương trình bậc nhất một ẩn?

A. 0x - 1 = 0;

B. x² + 2 = 0;

C. x + 0 = 0;

D. x + y = 0.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: C

+) 0x - 1 = 0

Vì a = 0 nên suy ra phương trình trên không là phương trình bậc nhất một ẩn

+) x² + 2 = 0

Þ Đây là phương trình bậc nhất hai ẩn

+) x + 0 = 0

Þ Đây là phương trình bậc nhất một ẩn

+) x + y = 0

Þ Đây không là phương trình bậc nhất một ẩn.

Câu 2:

Giá trị x = 2 là nghiệm của phương trình nào sau đây?

A. x + 2 = 0;

B. 2x - 2 = 0;

C. 2x + 2 = 0;

D. x - 2 = 0.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: D

+) x + 2 = 0

Û x = -2

Vậy nghiệm của phương trình là x = -2

+) 2x - 2 = 0

Û 2x = 2 Û x = 1

Vậy nghiệm của phương trình là x = 1

+) 2x + 2 = 0

Û 2x = -2 Û x = -1

Vậy nghiệm của phương trình là x = -1

+) x - 2 = 0

Û x = 2

Vậy nghiệm của phương trình là x = 2.

Câu 3:

Tập hợp nghiệm của phương trình (x + 3)(x - 1) = 0 là

A. S = {1};

B. S = {-3};

C. S = {1; -3};

D. S = {-1; 3}.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: C

(x + 3)(x - 1) = 0

$\Rightarrow [\begin{matrix} x + 3 = 0 \\ x - 1 = 0 \end{matrix} \Leftrightarrow [\begin{matrix} x = - 3 \\ x = 1 \end{matrix}$

Vậy tập hợp nghiệm của phương trình là S = {1; -3}.

Câu 4:

Điều kiện xác định của phương trình $\frac{2}{x - 2} = x$ là

A. x ¹ 2;

B. x ¹ -2;

C. x ¹ 2 và x ¹ 1;

D. x ¹ 2 và x ¹ 0.

Xem đáp án

Đáp án đúng là: A

Điều kiện xác định của phương trình $\frac{2}{x - 2} = x$ là

Û x - 2 ¹ 0 Û x ¹ 2.

Câu 5:

Bất phương trình x - 1 £ 0 tương đương với bất phương trình nào sau đây?

A. x £ 0;

B. x £ 1;

C. x ³ 0;

D. x £ -1.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: B

Ta có:

x - 1 £ 0 Û x £ 1

Hai bất phương trình tương đương là hai bất phương trình có chung tập nghiệm nên suy ra:

Bất phương trình x - 1 £ 0 tương đương với bất phương trình x £ 1.

Câu 6:

Tập nghiệm của bất phương trình 2x < 2 là

A. {x | x < 1};

B. {x | x < -1};

C. {x | x > 2};

D. {x | x < 2}.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: A

2x < 2 Û x < 1

Vậy suy ra tập nghiệm của bất phương trình là S = {x | x < 1}.

Câu 7:

Hình vẽ sau biểu diễn tập nghiệm của bất phương trình nào?

A. x £ 3;

B. x ³ 3;

C. x < 3;

D. x > 3.

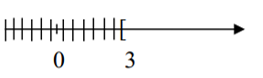
Xem đáp án

Hướng dẫn giải

Đáp án đúng là: B

Hình vẽ trên biểu diễn tập nghiệm của bất phương trình x ³ 3.

Câu 8:

Cho AB = 50 cm và CD = 10 dm; Tỉ số của hai đoạn thẳng AB và CD bằng

A. 5;

B. $\frac{1}{5}$

C. 2;

D. $\frac{1}{2}$

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: D

Ta có CD = 10 dm = 100 cm.

Tỉ số của hai đoạn thẳng AB và CD bằng:

$\frac{A B}{C D} = \frac{50}{100} = \frac{1}{2} .$

Câu 9:

Quan sát Hình 1, biết AD là đường phân giác của tam giác ABC. Tỉ số $\frac{D C}{D B}$ bằng tỉ số nào dưới đây?

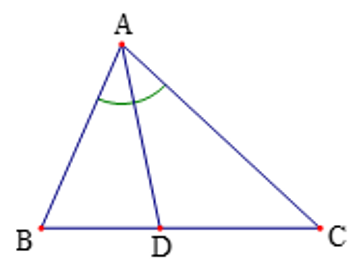
Quan sát Hình 1, biết AD là đường phân giác của tam giác ABC. Tỉ số DC/DB bằng tỉ số nào dưới đây? (ảnh 1)

A. $\frac{A C}{A B};$

B. $\frac{A B}{B C};$

C. $\frac{A B}{A C};$

D. $\frac{A C}{B C} .$

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: A

Ta có AD là đường phân giác của tam giác ABC.

Áp dụng tính chất đường phân giác vào tam giác ABC có:

$\frac{D C}{D B} = \frac{A C}{A B}$ .

Vậy tỉ số tỉ số $\frac{D C}{D B}$ bằng với tỉ số $\frac{A C}{A B} .$

Câu 10:

Cho ∆ABC, một đường thẳng a song song với BC cắt các cạnh AB và AC lần lượt ở D và E. Biết $\frac{A E}{E C} = \frac{1}{3}$ , tỉ số $\frac{D E}{B C}$ bằng

A. $\frac{1}{3};$

B. $\frac{2}{3};$

C. $\frac{1}{4};$

D. $\frac{4}{3} .$

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: C

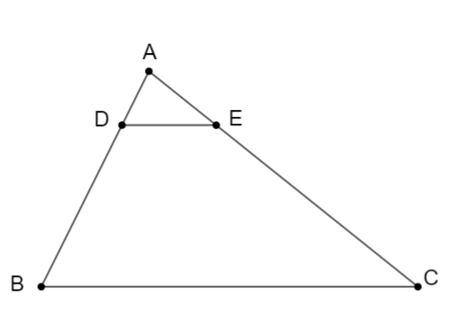
Cho ∆ABC, một đường thẳng a song song với BC cắt các cạnh AB và AC lần lượt ở D và E. (ảnh 1)

Ta có:

$\frac{A E}{E C} = \frac{1}{3} \Rightarrow \frac{A E}{A C} = \frac{1}{3 + 1} = \frac{1}{4}$

Với DE // BC. Áp dụng định lý Ta-lét vào tam giác ABC, ta có:

$\frac{D E}{B C} = \frac{A E}{A C} = \frac{1}{4}$ .

Vậy suy ra tỉ số $\frac{D E}{B C}$ bằng $\frac{1}{4}$

Câu 11:

Nếu ∆MNP đồng dạng với ∆ABC theo tỉ số $k = \frac{1}{2}$ thì tỉ số diện tích của tam giác MNP và diện tích tam giác ABC bằng

A. $\frac{1}{5};$

B. $\frac{1}{4}$

C. $\frac{1}{3}$

D. $\frac{1}{2}$

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: B

Với ∆MNP đồng dạng với ∆ABC thì tỉ số diện tích của tam giác MNP và diện tích tam giác ABC bằng bình phương tỉ số đồng dạng

$\Rightarrow \frac{S_{M N P}}{S_{A B C}} = k^{2} = {(\frac{1}{2})}^{2} = \frac{1}{4} .$

Câu 12:

Bóng của một cây cột cờ trên mặt đất có độ dài 4,8m; cùng thời điểm đó một thanh sắt vuông góc với mặt đất cao 1m có bóng dài 0,4m. Vậy chiều cao của cây cột cờ là

A. 10 m;

B. 11 m;

C. 12 m;

D. 13 m.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: C

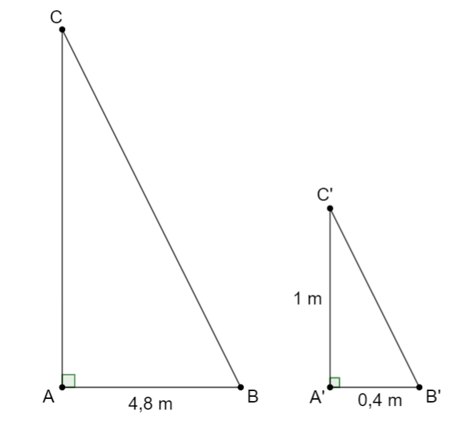
Bóng của một cây cột cờ trên mặt đất có độ dài 4,8m; cùng thời điểm đó một thanh sắt vuông góc (ảnh 1)

Gọi chiều cao cột điện là x (m) (x > 0).

Giả sử cột điện là AC, có bóng trên mặt đất là AB.

Thanh sắt là A'C', có bóng trên mặt đất là A'B'.

Vì cột điện và thanh sắt đều vuông góc với mặt đất nên hai tam giác ABC và A'B'C' đều là tam giác vuông.

Xét hai tam giác vuông DABC và DA'B'C' lần lượt vuông tại A và A' có

$\hat{B} = \hat{B'}$ (vì cùng một thời điểm tia sáng tạo với mặt đất một góc bằng nhau)

Nên suy ra DABC ᔕ ∆A'B'C' (g.g)

$\Rightarrow \frac{A C}{A' C'} = \frac{A B}{A' B'} \Leftrightarrow A C = \frac{A' C' . A B}{A' B'}$ .

$\Leftrightarrow A C = \frac{4,8.1}{0,4} = 12 (m)$

Vậy chiều cao của cây cột cờ là 12 m.

Câu 13:

Cho biết hình hộp chữ nhật ABCD.A'B'C'D' có AB = 3cm, BC = 5cm, AA’ = 4cm.

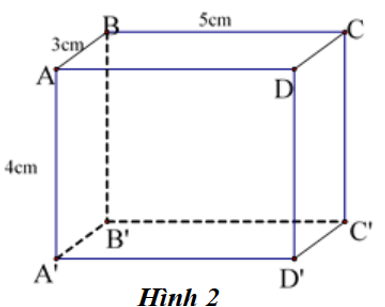
Đường thẳng C'D' song song với đường thẳng

A. A'B'.

B. BC.

C. AD.

D. AA'.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: A

Xét vào hình chữ nhật A'B'C'D' ta suy ra được đường thẳng C'D' song song với đường thẳng A'B'.

Câu 14:

Diện tích xung quanh của hình hộp chữ nhật ABCD.A'B'C'D' là

A. 15 cm²;

B. 20 cm²;

C. 32 cm²;

D. 64 cm².

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: D

Diện tích xung quanh của hình hộp chữ nhật ABCD.A'B'C'D' là

S_xq = S_ABB'A' + S_BCC'B' + S_CDD'C' + S_DAA'D'

= AB.BB' + BC.BB' + CD.DD' + AD.DD'

= 3.4 + 5.4 + 3.4 + 5.4 = 64 (cm²).

Vậy diện tích xung quanh của hình hộp chữ nhật ABCD.A'B'C'D' là 64 cm².

Câu 15:

Thể tích của hình hộp chữ nhật ABCD.A'B'C'D' là

A. 15 cm³;

B. 20 cm³;

C. 32 cm³;

D. 60 cm³.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: D

Thể tích của hình hộp chữ nhật ABCD.A'B'C'D' là:

V_{ABCD.A'B'C'D'} = AB.BC.AA' = 3.5.4 = 60 (cm³).

Vậy thể tích của hình hộp chữ nhật ABCD.A'B'C'D' là 60 cm³.

Câu 16:

a) Giải các phương trình sau:

1) 5x – 6 = 4.

Xem đáp án

Hướng dẫn giải

1) 5x – 6 = 4

Û 5x = 6 + 4

Û 5x = 10

Û x = 2

Vậy tập nghiệm của phương trình là S = {2}.

Câu 17:

a) Giải các phương trình sau:

2) $\frac{2 x}{x + 2} - 2 = \frac{x}{x + 2} .$

Xem đáp án

2)

ĐKXĐ: x + 2 ¹ 0 Û x ¹ -2

Þ x = -4 (TMĐK)

$\Leftrightarrow \frac{2 x - 2 (x + 2)}{x + 2} = \frac{x}{x + 2}$

$\Leftrightarrow \frac{2 x - 2 x - 4}{x + 2} = \frac{x}{x + 2}$

$\Leftrightarrow \frac{- 4}{x + 2} = \frac{x}{x + 2}$

Vậy tập nghiệm của phương trình là S = {-4}.

Câu 18:

b) Ông của Bình hơn Bình 61 tuổi. Bình tính rằng 6 năm nữa thì bốn lần tuổi Bình chỉ kém tuổi của Ông là 1 tuổi. Hãy tính tuổi của Bình hiện nay?

Xem đáp án

b) Gọi số tuổi của Bình là x (x > 0).

Hiện tại ông của Bình hơn Bình 61 tuổi nên số tuổi của ông Bình là x + 61 (tuổi)

Sau 6 năm nữa thì số tuổi của Bình là x + 6 và số tuổi của ông Bình là x + 67 (tuổi)

Khi đó, thì bốn lần tuổi Bình chỉ kém tuổi của Ông là 1 tuổi nên ta suy ra được phương trình:

4(x + 6) = (x + 67) - 1

Û 4x + 24 = x + 66

Û 4x - x = 66 - 24

Û 3x = 42

Û x = 14 (TMĐK)

Vậy năm nay Bình 14 tuổi.

Câu 19:

a) Giải bất phương trình sau và biểu diễn tập nghiệm trên trục số: 3x + 6 < 0.

Xem đáp án

Hướng dẫn giải

a) 3x + 6 < 0

Û 3x < -6 Û x < -2

Vậy tập nghiệm của bất phương trình là S = {-2}

Khi đó biểu diễn tập nghiệm trên trục số là

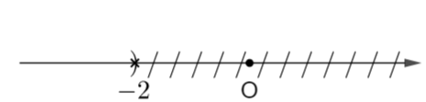
a) Giải bất phương trình sau và biểu diễn tập nghiệm trên trục số: 3x + 6 < 0. (ảnh 1)

Câu 20:

b) Cho biết a > b, chứng tỏ rằng 8a + 2022 > 8b + 2022.

Xem đáp án

b) a > b

Nhân hai vế của bất phương trình trên vưới 8 ta có:

Û 8a > 8b

Công hai vế của bất phương trình trên với 2022 nên suy ra:

Û 8a + 2022 > 8b + 2022 (đpcm)

Câu 21:

Cho tam giác ABC vuông tại A, đường cao AH (H Î BC).

a) Chứng minh ∆ABC đồng dạng với ∆HAC, từ đó suy ra AC² = BC.HC.

Xem đáp án

Hướng dẫn giải

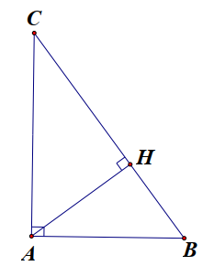
Cho tam giác ABC vuông tại A, đường cao AH (H thuộc BC). a) Chứng minh ∆ABC đồng dạng với ∆HAC, từ đó suy ra AC2 = BC.HC. (ảnh 1)

a) Xét hai tam giác ∆ABC và ∆HAC có

$\begin{matrix} \hat{A C B} = \hat{H C A} (\hat{A} c h u n g) \\ \hat{B A C} = \hat{A H C} (= 90 °) \end{matrix}\} \Rightarrow Δ A B C ∽ Δ H A C (g . g)$

\Rightarrow \frac{A H}{H C} = \frac{B C}{A C} \Leftrightarrow A C^{2} = B C . H C

(đpcm)

Câu 22:

b) Cho biết HB = 9 cm, HC = 16 cm. Tính độ dài các cạnh AB, AC của ∆ABC.

Xem đáp án

b) Ta có: BC = HB + HC = 9 + 16 = 25 (cm)

+) AC² = BC.HB (cmt)

$\Rightarrow A C = \sqrt{B C . H B} = \sqrt{25.9} = 15 (c m)$

Áp dụng định lý Py-ta-go vào tam giác ABC vuông tại A có:

$A B = \sqrt{B C^{2} - A C^{2}} = \sqrt{25^{2} - 15^{2}} = 20 (c m) .$

Vậy AB = 20 cm; AC = 15 cm.