Đề kiểm tra cuối kỳ 2 Toán 8 có đáp án ( Mới nhất)_ đề 2
-
6047 lượt thi
-
10 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Hình hộp chữ nhật là hình có bao nhiêu mặt?
Xem đáp án
Hình hộp chữ nhật là hình gồm có 8 đỉnh , 6 mặt , 12 cạnh.
Vậy chọn đáp án B.
Câu 3:
Tập nghiệm của phương trình x(x + 1) = 0 là:
Xem đáp án
Ta có: x(x + 1) = 0
Û x = 0 hoặc x + 1 = 0
Û x = 0 hoặc x = − 1.
Do đó, tập nghiệm của phương trình đã cho là S = {0; –1}.
Vậy chọn đáp án B.
Câu 4:
Bất phương trình nào sau đây là bất phương trình bậc nhất một ẩn?
Xem đáp án
Bất phương trình ẩn x là hệ thức A (x) > B (x) hoặc A (x) < B (x) hoặc A (x) ≥ B (x) hoặc A (x) ≤ B (x). Trong đó: A (x) gọi là vế trái; B(x) gọi là vế phải.
Ta có:
• Bất phương trình x + y > 8 có vế trái là đa thức có chứa hai ẩn, vế phải là hằng số.
Do đó, x + y > 8 không phải là bất phương trình bậc nhất một ẩn.
• Bất phương trình 0x + 5 ≥ 0 có vế trái là hằng số (vì 0x + 5 = 5) và vế phải cũng là hằng số.
Do đó, 0x + 5 ≥ 0 không phải là bất phương trình bậc nhất một ẩn.
• Bất phương trình x – 3 > 4 có vế trái là đa thức bậc nhất một ẩn, vế phải là hằng số.
Do đó, x – 3 > 4 là bất phương trình bậc nhất một ẩn.
• Bất phương trình (x – 7)2 ≤ 6x có vế phải là đa thức bậc hai, vế phải là hằng số.
Do đó, (x – 7)2 ≤ 6x là bất phương trình bậc nhất một ẩn.
Vậy chọn đáp án C.
Câu 5:
Hình sau biểu diễn tập nghiệm của bất phương trình nào?
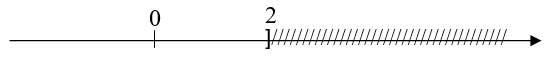
Xem đáp án
Hình vẽ trên biểu diễn tập nghiệm của bất phương trình x £ 2.
Vậy chọn đáp án B.
Câu 6:
Trong các khẳng định sau, khẳng định nào không đúng?
Xem đáp án
Các khẳng định A, B, D là khẳng định đúng.
Còn khẳng định C sai vì các cạnh bên của hình lăng trụ đứng bằng nhau.
Vậy chọn đáp án C.
Câu 7:
Giải các phương trình và bất phương trình sau:
a) (x – 2)(x + 7) = 0;
b) .
Xem đáp án
a) (x – 2)(x + 7) = 0
Û x – 2 = 0 hoặc x + 7 = 0
Û x = 2 hoặc x = −7.
Vậy tập nghiệm của phương trình đã cho là S = {2; −7}.
b)
Û 4x + 7 – 30x ≥ 9
Û 4x – 30x ≥ 9 – 7
Û – 26x ≥ 2
.
Vậy tập nghiệm của bất phương trình đã cho là .
Câu 8:
Một vòi nước chảy vào bể không có nước. Cùng lúc đó một vòi nước khác chảy từ bể ra. Mỗi giờ lượng nước vòi chảy ra bằng 
lượng nước chảy vào. Sau 5 giờ thì bên trong bể đạt tới 
dung tích bể. Hỏi nếu bể không có nước mà chỉ mở vòi chảy vào thì sau bao lâu thì đầy bể?
Xem đáp án
Gọi x (giờ) là thời gian vòi chảy vào bể từ khi chưa có nước đến khi đầy bể (x > 0).
Trong 1 giờ, vòi đó chảy được số phần bể là: bể.
Trong 1 giờ, vòi chảy ra chiếm số phần bể là: bể.
Sau 5 giờ thì bên trong bể đạt tới 
dung tích bể nên ta có phương trình:
x = 8 (TMĐK).
Vậy thời gian vòi chảy vào bể từ khi chưa có nước đến khi đầy bể là 8 giờ.
Câu 9:
Cho hình chữ nhật ABCD có AB = 8 cm; BC = 6 cm. Vẽ đường cao AH của ∆ADB.
a) Chứng minh: ∆AHB đồng dạng ∆BCD.
b) Chứng minh: AD2 = DH . DB.
c) Tính độ dài đoạn thẳng AH.
Xem đáp án
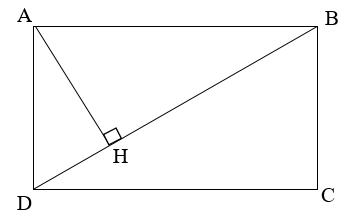
a) Vì ABCD là hình chữ nhật nên AB // CD.
Suy ra: (hai góc so le trong).
Xét ∆AHB và ∆BCD có:
(cmt).
Do đó ∆AHB 
∆BCD (g.g).
b) Xét ∆AHD và ∆BAD có:
chung.
Do đó ∆AHD ∆BAD (g.g)
Suy ra .
Vậy AD2 = DH . BD (đpcm).
c) Xét ∆ABD vuông tại A, áp dụng định lý Py-ta-go, ta có:
BD2 = AB2 + AD2 = 82 + 62 = 100
Suy ra: BD = 10 (cm)
Từ câu a: ∆AHB ∆BCD suy ra .
Hay AH . BD = AB. BC.
Do đó (cm).
Vậy AH = 4,8 cm.
Câu 10:
Xem đáp án
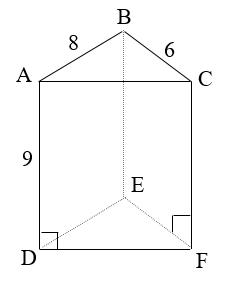
Độ dài hai cạnh góc vuông là 6 cm và 8 cm nên ∆ABC vuông tại B.
Ta có: (theo định lý Py-ta-go).
Diện tích xung quanh của hình lăng trụ đứng là:
Sxq = (6 + 8 + 10) . 9 = 216 (cm2).
Diện tích một mặt đáy của hình lăng trụ đứng là:
(cm2).
Diện tích toàn phần của hình lăng trụ đứng là:
Stp = Sxq + S2đ = 216 + 2 . 24 = 264 (cm2).
Vậy diện tích toàn phần của hình lăng trụ 264 cm2.