10 câu hỏi trắc nghiệm thuộc Đề kiểm tra cuối kỳ 2 Toán 8 có đáp án ( Mới nhất)_ đề 24

Câu 1:

Giải phương trình

a) 8x - 5 = 3(x - 6) + 7

Xem đáp án

Hướng dẫn giải

a) 8x - 5 = 3(x - 6) + 7

Û 8x - 5 = 3x - 18 + 7

Û 8x - 3x = 5 - 18 + 7

Û 5x = -6

Vậy nghiệm của phương trình là $x = \frac{- 6}{5} .$

Câu 2:

Giải phương trình

b) $\frac{x - 2}{6} - \frac{x}{2} = \frac{5 - 2 x}{3}$

Xem đáp án

b) $\frac{x - 2}{6} - \frac{x}{2} = \frac{5 - 2 x}{3}$

\Leftrightarrow \frac{x - 2}{6} - \frac{3 x}{6} = \frac{2 (5 - 2 x)}{6}

$\Leftrightarrow \frac{x - 2 - 3 x}{6} = \frac{10 - 4 x}{6}$

$\Leftrightarrow \frac{- 2 x - 2}{6} = \frac{10 - 4 x}{6}$

Þ -2x - 2 = 10 - 4x

Û -2x + 4x = 10 + 2

Û 2x = 12

Û x = 6

Vậy nghiệm của phương trình là x = 6.

Câu 3:

Giải phương trình

c) x² - 16 + 5x(x - 4) = 0

Xem đáp án

c) x² - 16 + 5x(x - 4) = 0

Û x² - 16 + 5x² - 20x = 0

Û 6x² - 20x - 16 = 0

Û 3x² - 10x - 8 = 0

Û 3x² - 12x + 2x - 8 = 0

Û 3x(x - 4) + 2(x - 4) = 0

Û (3x + 2)(x - 4) = 0

$\Rightarrow [\begin{matrix} 3 x + 2 = 0 \\ x - 4 = 0 \end{matrix} \Leftrightarrow [\begin{matrix} x = \frac{- 2}{3} \\ x = 4 \end{matrix}$

Vậy tập nghiệm của phương trình là $S = \{\frac{- 2}{3}; 4\} .$

Câu 4:

Giải phương trình

d) $\frac{5 x}{x - 3} + \frac{2}{x + 3} = \frac{x^{2} + 5 x - 6}{x^{2} - 9}$

Xem đáp án

d) ĐKXĐ: $\{\begin{matrix} x - 3 \neq 0 \\ x + 3 \neq 0 \end{matrix} \Leftrightarrow \{\begin{matrix} x \neq 3 \\ x \neq - 3 \end{matrix}$

$\frac{5 x}{x - 3} + \frac{2}{x + 3} = \frac{x^{2} + 5 x - 6}{x^{2} - 9}$

\Leftrightarrow \frac{5 x}{x - 3} + \frac{2}{x + 3} = \frac{x^{2} + 5 x - 6}{(x - 3) (x + 3)}

$\Leftrightarrow \frac{5 x (x + 3)}{(x - 3) (x + 3)} + \frac{2 (x - 3)}{(x - 3) (x + 3)} = \frac{x^{2} + 5 x - 6}{(x - 3) (x + 3)}$

$\Leftrightarrow \frac{5 x^{2} + 15 x}{(x - 3) (x + 3)} + \frac{2 x - 6}{(x - 3) (x + 3)} = \frac{x^{2} + 5 x - 6}{(x - 3) (x + 3)}$

$\Leftrightarrow \frac{5 x^{2} + 17 x - 6}{(x - 3) (x + 3)} = \frac{x^{2} + 5 x - 6}{(x - 3) (x + 3)}$

Þ 5x² + 17x - 6 = x² + 5x - 6

Û 4x² + 12x = 0

Û 4x(x + 3) = 0

$\Rightarrow [\begin{matrix} x = 0 \\ x + 3 = 0 \end{matrix}$

$\Leftrightarrow [\begin{matrix} x = 0 \\ x = - 3 \end{matrix}$

Đối chiếu ĐKXĐ suy ra x = 0 thỏa mãn

Vậy nghiệm của phương trình là x = 0.

Câu 5:

Một ô tô đi từ Thành phố Hồ Chí Minh đến Quy Nhơn với vận tốc trung bình là 80 km/h. Khi đi từ Quy Nhơn về Thành phố Hồ Chí Minh, xe tăng vận tốc thêm 10 km/h nên thời gian về ít hơn thời gian đi 48 phút. Tính quãng đường Thành phố Hồ Chí Minh đi Quy Nhơn?

Xem đáp án

Hướng dẫn giải

Gọi x (km) là độ dài quãng đường từ Thành phố Hồ Chí Minh đến Quy Nhơn (x > 0)

Thời gian ô tô đi từ Thành phố Hồ Chí Minh đến Quy Nhơn với vận tốc 80 km/h là $\frac{x}{80} h$ .

Ô tô đi từ Quy Nhơn về Thành phố Hồ Chí Minh với vận tốc lớn hơn lúc đi 10 km/h tức là 90 km/h với số thời gian là $\frac{x}{90} h$ .

Do thời gian về ít hơn thời gian đi là 48 phút tức là ít hơn $\frac{48}{60} = \frac{4}{5} h$ nên ta có phương trình:

\frac{x}{80} - \frac{x}{90} = \frac{4}{5}

$\Leftrightarrow \frac{6 x}{300} - \frac{5 x}{300} = \frac{2}{5}$

$\Leftrightarrow \frac{6 x - 5 x}{300} = \frac{x}{300} = \frac{2}{5}$

$\Leftrightarrow x = 300. \frac{2}{5} = 120 (T M Đ K) .$

Vậy quãng đường Thành phố Hồ Chí Minh đi Quy Nhơn là 120 km.

Câu 6:

Giải bất phương trình và biểu diễn tập nghiệm trên trục số:

$\frac{2 x - 1}{3} - 2 \geq \frac{x}{5}$ .

Xem đáp án

Hướng dẫn giải

$\frac{2 x - 1}{3} - 2 \geq \frac{x}{5}$

$\Leftrightarrow \frac{2 x - 1 - 6}{3} \geq \frac{x}{5}$

$\Leftrightarrow \frac{2 x - 7}{3} \geq \frac{x}{5}$

Û 5(2x - 7) ³ 3x

Û 10x - 35 ³ 3x

Û 10x - 3x ³ 35

Û 7x ³ 35

Û x ³ 5

Vậy tập nghiệm của phương trình là S = {x | x ³ 5}.

Khi đó ta có biểu diễn của tập nghiệm trên trục số là:

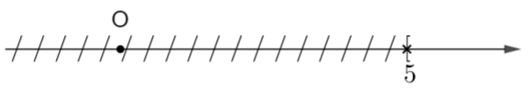
Giải bất phương trình và biểu diễn tập nghiệm trên trục số: . (ảnh 1)

Câu 7:

Một ngôi nhà có thiết kê mái như hình vẽ và các số đo như sau: AD = 1,5 m; DE = 2,5 m; BF = GC = 1 m; FG = 5,5 m. Tính chiều dài của mái nhà bên, biết DE // BC.

Một ngôi nhà có thiết kê mái như hình vẽ và các số đo như sau: AD = 1,5 m; DE = 2,5 m; BF = GC = 1 m; FG = 5,5 m. (ảnh 1)

Xem đáp án

Hướng dẫn giải

Ta có: BC = BF + FG + GC = 1 + 5,5 + 1 = 7,5 (m).

Xét tam giác ABC, áp dụng định lý Ta-lét, ta có:

Với DE // BC, ta có: $\frac{D E}{B C} = \frac{A D}{A B}$

$\Leftrightarrow \frac{2,5}{7,5} = \frac{1,5}{A B} \Leftrightarrow A B = \frac{1,5.7,5}{2,5} = 4,5 (m)$ .

Vậy chiều dài của mái nhà bên là 4,5 m.

Câu 8:

Cho DABC vuông tại A, đường cao AH (H thuộc BC). Biết AB = 18 cm, AC = 24 cm.

a) Chứng minh: AB² = BH.BC.

Xem đáp án

Hướng dẫn giải

Cho ABC vuông tại A, đường cao AH (H thuộc BC). Biết AB = 18 cm, AC = 24 cm. a) Chứng minh: AB2 = BH.BC. (ảnh 1)

a) Xét hai tam giác DABH và DCBA có:

$\begin{matrix} \hat{A B H} = \hat{C B A} (\hat{B} c h u n g) \\ \hat{A H B} = \hat{C A B} (= 90 °) \end{matrix}\} \Rightarrow Δ A B H ∽ Δ C B A (g . g)$

$\Rightarrow \frac{A B}{C B} = \frac{B H}{B A} \Leftrightarrow A B^{2} = B H . B C$ (đpcm)

Câu 9:

b) Kẻ đường phân giác CD của DABC (D thuộc AB). Tính độ dài DA.

Xem đáp án

b) Áp dụng định lý Pytago vào tam giác ABC vuông tại A có:

$B C = \sqrt{A B^{2} + A C^{2}} = \sqrt{18^{2} + 24^{2}} = 30 c m$

Áp dụng tính chất đường phân giác với CD là đường pgaan giác trong của góc C

$\Rightarrow \frac{D A}{B D} = \frac{A C}{B C} = \frac{24}{30} = \frac{4}{5} \Leftrightarrow B D = \frac{5}{4} . D A$

Lại có:

BD + DA = BA = 18 (cm)

$\Leftrightarrow \frac{5}{4} . D A + D A = 18$

$\Leftrightarrow \frac{9}{4} D A = 18 \Leftrightarrow D A = 18. \frac{4}{9} = 8 (c m) .$

Câu 10:

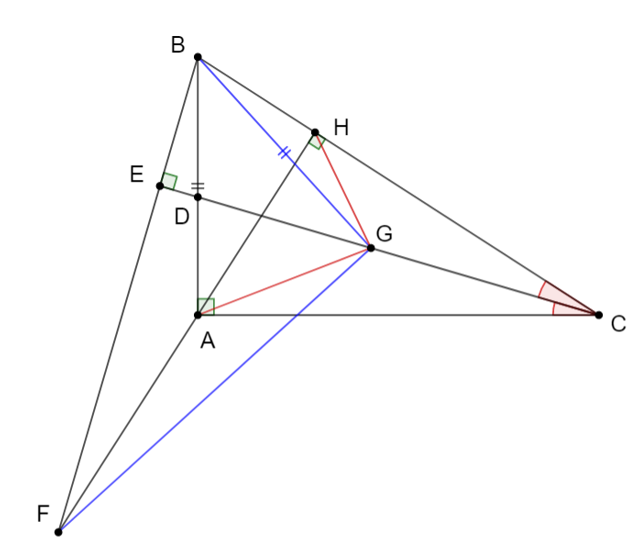
c) Từ B kẻ đường thẳng vuông góc với đường thẳng CD tại E và cắt đường thẳng AH tại F. Trên đoạn thẳng CD lấy điểm G sao cho BA = BG.

Chứng minh: BG ^ FG.

Xem đáp án

c) Ta có: BA = BG

+) $\frac{A B}{C B} = \frac{B H}{B A} (c m t) \Rightarrow \frac{B G}{C B} = \frac{B H}{B G}$

Û BG² = BH.BC (1)

+) Xét hai tam giác DEBC và DHBF có:

$\begin{matrix} \hat{B E C} = \hat{B H F} (= 90 °) \\ \hat{E B C} = \hat{H B F} (\hat{B} c h u n g) \end{matrix}\} \Rightarrow Δ E B C ∽ Δ H B F (g . g)$

$\Rightarrow \frac{B H}{B E} = \frac{B F}{B C} \Leftrightarrow B H . B C = B E . B F$ (2)

Từ (1) và (2) Þ BG² = BE.BF

$\Leftrightarrow \frac{B G}{B E} = \frac{B F}{B F}$

+) Xét hai tam giác DBGE và DBFG có

$\begin{matrix} \frac{B G}{B E} = \frac{B F}{B F} (c m t) \\ \hat{E B G} = \hat{G B F} (\hat{B} c h u n g) \end{matrix}\} \Rightarrow Δ B G E ∽ Δ B F G (c . g . c)$

$\Rightarrow \hat{B E G} = \hat{B G F}$ (Hai góc tương ứng)

Mà $\hat{B E G} = \hat{B E C} = 90 °$ . Nên suy ra $\hat{B G F} = 90 °$

Vậy suy ra BG ^ FG (đpcm).